 |
| Trigonometric circle sine cosine |
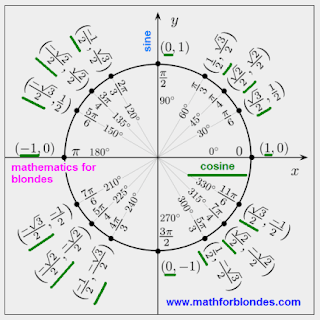
As I always become confused during translation of co-ordinates of points of circumference in sine and cosine, for simplicity all values of cosines (cos) for corners from 0 to 360 degrees (from 0 pi there is to 2 pi rad) are underline a green hyphen. Even at unsealing of this picture of trigonometric circle on a not coloured printer all values of cosine will be underline, and values of sine will be without underlining.
Opposite the indicated corners on a circumference points are located, and the coordinates of these points are indicated in parentheses. The coordinate of Х is writtenin the first.
Let us conduct a survey excursion on this corner of mathematical zoo. Foremost, it is needed to mark that is here present the Euclidean system of coordinates is Cartesian is one black horizontal line with the letter of Х near a pointer, second is a vertical with a letter Y. On the axis of Х, which is yet named abscise axis (this clever word of mathematics was thought of specially, what to tangle blondes) cosine live, - cos. On an axis Y, which is named y-axis (another clever word which in the mouths of blonde can become a killing weapon), sine live - sin. If to look at domestic life of these trigonometric functions, then it is not difficult to notice that sine always on a kitchen at a flag for vertical lines, and cosine - on a sofa before a television set on a horizontal.
In this system of coordinates a circumference is drawn by a radius, equal to unit. A centre of circumference is at the beginning of the system of co-ordinates - wherein abscise axis (axis of Х) and ordinates (axis of У) intersect in the centre of picture.
From the center of circumference thin hyphens which show corners 30 are conducted, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 degrees. In the radian measure of corners this pi/6, pi/4, pi/3, 2pi/3, 3pi/4, 5pi/6, 7pi/6, 5pi/4, 4pi/3, 3pi/2, 5pi/3, 7pi/4, 11pi/6. With the axes of coordinates such values of corners coincide: 0, 90, 180, 270 degrees or 0 pi, pi/2, pi, 3pi/2. Using a picture, it is very simple to transfer corners from degrees in radians and from radian in degrees. Identical values in the different systems of goniometry are written on one line, representing this corner.
The lines of corners end with points on a single circumference. Near every point, in round собках, the coordinates of this point are writtenin. The coordinate of Х, which corresponds to the cosine of corner, forming this point, is writtenin the first. The coordinate is writtenin the second Y this point, that corresponds to the value of sine of corner. On a picture easily enough to find a sine and cosine of the set corner and vice versa, by set value of sine or cosine, it is possible easily to find the value of corner. Mainly, not to entangle a sine with a cosine.
I watch out for circumstance that if you by value search a sine or cosine corner, it is necessarily needed to finish writing the period of corner. Mathematicians very athrob behave to this appendicitis of trigonometric functions and at his absence can stick in two after, it would seem, right answer. What period at determination of corner by value to the trigonometric function? It is such piece which is thought of mathematicians specially in an order to be tangled and tangle other. Especially blondes. But about it we will talk somehow other time.
All, that it is collected in a small group on the picture of trigonometric circle of sine and cosine, it is possible attentively to consider on separate pictures with the portraits of sine 0, 30, 45 degrees (reference to the separate pages I will add as far as the increase of photo gallery of sine and cosine).
Automatic translation from Russian.
On this page you will find: cos sin tabel 30, 45, 60, 90. Function for student: sin60, sine cosine of 0 45 30 60 90 180 270 360. Table 2 pi to 360 values of trigonometric identities. Table of values of sine function, sin cos 60 30 45. Table of degrees to radians 0 to 2pi with sines and cosines. cos sin pi for student: 0pi, pi/6, pi/4, pi/3, pi/2, 2pi/3, 3pi/4, 5pi/6, pi, 7pi/6, 5pi/4, 4pi/3, 3pi/2, 5pi/3, 7pi/4, 11pi/6, 2pi. sin pi/4 table values, sin = 3pi / 2/ Tabel trigonometri 360 derajat, the value of sin 3pi/2 - cos pi/3. Trigonometric circle illustration.
How to find a decision:
Sines and cosines are a circle - here picture in all trigonometric beauty.
Corner 120 degrees in radians - equal 2/3 pi or 2 pi divided by 3, it is very beautifully drawn on a picture.
Values of sines of cosines of corners are in radians - there are such on a picture, I hope, exactly those corners that you search.
Value of cosine of corner in 45 degrees - equal a root is square from two divided by two, can check on a picture.
Trigonometric circumference - I am not quite sure that the circumference presented on a picture is trigonometric, but something from trigonometry in this circumference there are certainly, for example, sines and cosines on a circumference is the outpoured trigonometry.
A trigonometric circle is a picture - I am here such. Indeed, most not beautiful picture, it is possible to draw much more beautiful and clearer. To me minus in reputation - why did not I until now draw him for blondes? you present a situation in the art gallery of the future : a tour guide explains to the group of schoolchildren "Before you known worldwide picture "Trigonometric Madonna with an unit segment on hands" is a picture of genius artist of Early Mathematical Renaissance ." age. Farther she names the name of this artist (he or she).This name can be your!
Circle of sines and cosines - a just the same circle quite by chance appeared here on a picture.
Corner 9 degrees how many it in pi - in pi it 1/20 or pi/20.
Decision: for translation of degrees in pi radian, it is needed to divide present for us degrees into 180 degrees (this 1 pi is a radian). 9/180 = 1/20 turns out for us.
Answer: 9 degrees = 1/20 pi.
Unit circle degrees and radians marked for units of pie - it here in blonde math.















After a nice career as a metallurgical engineer in the steel industry, I started teaching high school geometry this past academic yr. Stumbled across your site, and really love it. I'll definitely be back and recommend it to my students. -KarlH - Indiana, US
ReplyDeleteThank you very much for your feedback. I am a civil engineer and still work. I have been studying math for 15 years out of curiosity. Nikolay, Krivoy Rog, Ukraine.
Delete