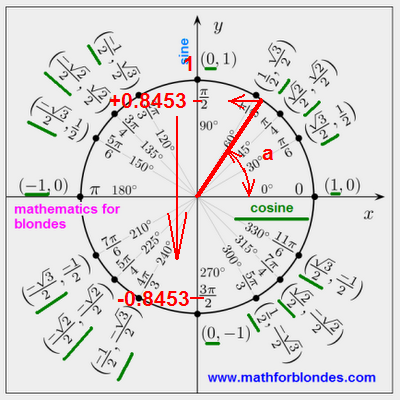
We must find a sine x with minus, a value is equal -0.8453
sin x = -0.8453
On the table of sines we find the value of corner in degrees and minutes for x, equal +0.8453. This corner is in limits from 0 to 90 degrees and equal 54 degrees 42 minutes.
sin a = +0.8453
a = 57 degrees 42 minutes
Farther we look a trigonometric circle and find a corner a. The positive values of sine are located in the overhead half of circle, negative values will be situated in the underbody of trigonometric circle.
One value of sine always has two values of corner. We will find these corners for the negative value of sine.
The first corner we will get, if to the corner a we will add 180 degrees. The second corner we will get, if from 360 degrees we will take away a corner a.
x1 = 180 degrees + a
x1 = 180 degrees + 57 degrees 42 minutes
x1 = (180 + 57) degrees 42 minutes
x1 = 237 degrees 42 minutes
x2 = 360 degrees - a
x2 = 360 degrees - 57 degrees 42 minutes
x2 = 359 degrees 60 minutes - 57 degrees 42 minutes
x2 = (359 - 57) degrees (60 - 42) minutes
x2 = 302 degrees 18 minutes
This was explanation, how to find a sine x with minus. Now a decision needs to be written down in accordance with bureaucratic rules that I do not know. It looks approximately so.
sin x = -0.8453
x = arcsin (-0.8453)
x1 = 237 degrees 42 minutes
x2 = 302 degrees 17 minutes
Saturday, September 29, 2012
Thursday, September 13, 2012
Phlogiston theory and complex numbers
At the beginning of XVIII century the theory of phlogiston appeared in chemistry and explained the process of burning the presence of "a fiery substance" to combustibles. It was believed that when the material is burned, it disappears from the phlogiston. For its time it was the most advanced theory, the first theory in the history of chemistry, through which chemicals become a science.
In the development of this theory, there was such a paradox: in chemical experiments on calcination have found that scale weighs more than the metal itself. Instead, that would decrease the mass scale increases when the metal is released phlogiston. Here come to the aid of physics mathematics with its negative numbers. The logic was clear - if there are positive and negative numbers, so there is a positive and negative mass. The theory of phlogiston recorded that phlogiston has negative mass, which is confirmed by experiments - negative weight of phlogiston leaves the metal and enters the air, resulting in a positive mass scale increases.
Thanks to the work of Antoine Lavoisier was digging the role of oxygen in the combustion process and replaced the phlogiston theory came the oxygen theory of combustion. In the new theory, the increase in mass scale was explained in the positive numbers: the weight of the metal added weight of oxygen from the air, resulting in a mass scale increases. That's so simple and effective negative numbers were expelled from chemistry. Because of this, today we enjoy the benefits of chemistry in the form in which they exist.
But physics lurking different fate. Where did the complex numbers? From the same place there was a weight of phlogiston - of negative numbers. This is the common parent of the two theories are even conduct DNA analysis is not necessary. Why is this? To understand this, one must look at the history of mathematics.
In the development of this theory, there was such a paradox: in chemical experiments on calcination have found that scale weighs more than the metal itself. Instead, that would decrease the mass scale increases when the metal is released phlogiston. Here come to the aid of physics mathematics with its negative numbers. The logic was clear - if there are positive and negative numbers, so there is a positive and negative mass. The theory of phlogiston recorded that phlogiston has negative mass, which is confirmed by experiments - negative weight of phlogiston leaves the metal and enters the air, resulting in a positive mass scale increases.
Thanks to the work of Antoine Lavoisier was digging the role of oxygen in the combustion process and replaced the phlogiston theory came the oxygen theory of combustion. In the new theory, the increase in mass scale was explained in the positive numbers: the weight of the metal added weight of oxygen from the air, resulting in a mass scale increases. That's so simple and effective negative numbers were expelled from chemistry. Because of this, today we enjoy the benefits of chemistry in the form in which they exist.
But physics lurking different fate. Where did the complex numbers? From the same place there was a weight of phlogiston - of negative numbers. This is the common parent of the two theories are even conduct DNA analysis is not necessary. Why is this? To understand this, one must look at the history of mathematics.
Wednesday, September 12, 2012
Trigonometry formulas multiple angles



Formulas in trigonometry multiple angles enjoy. There is a sine, cosine, tangent and cotangent double, triple, multiple arguments. In simple words, sin, cos, tg, ctg two alpha, alpha three, four and five alpha.
For all of the double angle formulas are written continuously through equality. In simplifying trigonometric expressions, these formulas taken as read from left to right and right to left in any order. Such a method of making the right formula is called the "method of sewing." Cut a piece of it, there is a piece, sewn together by an equal sign = Get ready-made formula. Cut to full expression, from one of the equal sign to the other. The drafters of the tasks do so. Or something like that then can think of to confuse you more.
Why are these formulas of trigonometry? To simplify trigonometric expressions, which complicated the task compilers. Perhaps they need more in some cases, but it's hard to come up with such. It is necessary to ask the physicists and engineers, whether they had to use these formulas.
Thursday, September 06, 2012
Basic trigonometric identities formula

Basic trigonometric identities of the formula is the basis of trigonometry. First formula circled outline in red wine, called basic trigonometric identities. Actually it is the Pythagorean theorem for trigonometric functions.
Two other formulas identities are obtained if the first equation divided by the square of the cosine of the angle alpha, or the square of the sine of that angle. The last formula is the trigonometric form of the basic properties of all the numbers: if the number is multiplied by the inverse number (or divided by the same number, which is the same thing) the result is a unit.
All the other bells and whistles this trigonometric formulas for basic trigonometric identities and definitions of trigonometric functions. No matter what corner of the universe you are, no matter what with the extraterrestrial civilizations did not communicate, basic trigonometry all be the same. Just do not want to write his formula, trying to prove that you are a human being. For any alien all these equations and symbols the same as that for you Chinese characters. Geometry - that a language that can easily do without interpreters to communicate with any intelligent creature from any planet. Animals are not able to understand the language of geometry. Of course, before you communicate in the language of geometry, it is necessary to learn the language by use.
Where does the basic trigonometric identities? Here's the "Legend of the sine and cosine," in which I explained his version of the occurrence of a trigonometric miracle.
Degree trigonometric functions formula

Degree trigonometric functions formula - very crib in the study of trigonometric functions. Here are the squares, cubes, and fourth-degree sine, cosine, tangent, cotangent. Still, these formulas can be called the degree of reduction formulas of trigonometric functions. In mathematics, like juggling different formulas, the formulas of trigonometry is just for the occasion.
If you take a particular angle, you will find it to trigonometric functions of the formulas, and then substitute these values into the formula and the appropriate calculations, the left and right sides you should get the same. What, in fact, says equality.
Wednesday, September 05, 2012
Matrix in mathematics
Matrix in mathematics perform quite a significant role. With the theory of matrix magic sort it out themselves on your textbooks. I want now to reason about sense of the matrix numbering. Many people know that the matrix used to solve systems of linear equations and matrices used for these purposes. I will not repeat the textbooks, and I suggest you go to kindergarten and there to look for the meaning of mathematical operations with matrices.
So, we will think of the simplest child's task about dogs and cats: "Now in zoosalone 2 cats 3 dogs clipped their wool. While 4 cats and 5 dogs are waiting in the queue. So how many cats and dogs want to change their image?" Simple task on two independent mathematical actions: add up the cats to the cats, add up the dogs to the dogs and get the result two numbers. One of which is the number of the cats, and the second the number of the dogs. That is simply. Now we will solve this task with the use of the matrix numbering on the calculator matrices.
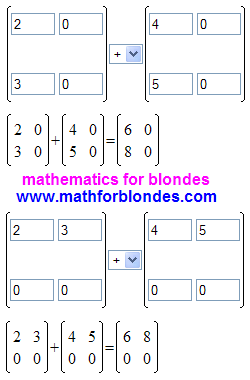
Here's what happened. As creators of calculator consider that operations with row vectors and column vectors are too primitive for mathematical knowledge of such high level, I had to go to a trick. The missing elements of square matrix the second order (this is the minimum size for the calculator matrices) I replaced with zeros.
On a picture it is shown that, I decided this task two methods: first, the values were in the first column, and then I put the same values in the first row of the matrix. Both variants gave the right result. From this we can conclude that the mathematical matrix operations within the meaning of a concurrent execution of mathematical operations with variables that have different units of measure.
In drawing up the matrix to solve a system of linear equations as a unit of measurement to take a unknown. For example, a unit of the decimal number system (just a number, the constant term of the equation), x, y, z, XXL ... Oh! It not from here, this unit is used to measure blouses. By the way, if you write in a matrix the number of your blouses, the matrix of this does not hurt - it does not matter what or where you are writing. But the correct solution to a system of equations with the matrix in the blouse you have not come out.
The principle of a matrix of equations for you take the numerical coefficients before unknown and inscribe them each into the place. That is where the matter of what and where exactly do you fit into the matrix. Then the resulting matrix solving.
Where is yet used principle of mathematical operations with matrices? When you count a whole bunch of money in paper notes and coins. Laid out bills and coins into piles on the dignity and recalculate the number in each pile. On this matrix method ends, farther you bring the got results to a single unit of measurement. Naturally, performing similar actions in everyday life, we never think about how it can be described mathematically.
Remember, we talked about the meters and decimetres? About bows and flounces, on a multi-core processor? There also can be used matrix methods of addition and subtraction. Perform all actions with the same unit of measurement, then all of the other unit of measurement. In the end, if necessary, make conversion between different units of measurement to another.
This method is very good to use in geodesy, when you need to add or subtract a large number of angles in degrees, minutes, seconds. Doing all the actions in degrees, then a minute, then with seconds. And then all received converting seconds into minutes and seconds. To obtain the minute add or subtract those moments obtained after converting seconds. Convert the result to degrees and minutes. To add on the total number of degrees degrees of minutes. All you have turned a corner in degrees, minutes, seconds.
I hope this article will be useful in practice, and you're using methods of matrix computations is in full knowledge of what you are doing and what the result will get.
So, we will think of the simplest child's task about dogs and cats: "Now in zoosalone 2 cats 3 dogs clipped their wool. While 4 cats and 5 dogs are waiting in the queue. So how many cats and dogs want to change their image?" Simple task on two independent mathematical actions: add up the cats to the cats, add up the dogs to the dogs and get the result two numbers. One of which is the number of the cats, and the second the number of the dogs. That is simply. Now we will solve this task with the use of the matrix numbering on the calculator matrices.

Here's what happened. As creators of calculator consider that operations with row vectors and column vectors are too primitive for mathematical knowledge of such high level, I had to go to a trick. The missing elements of square matrix the second order (this is the minimum size for the calculator matrices) I replaced with zeros.
On a picture it is shown that, I decided this task two methods: first, the values were in the first column, and then I put the same values in the first row of the matrix. Both variants gave the right result. From this we can conclude that the mathematical matrix operations within the meaning of a concurrent execution of mathematical operations with variables that have different units of measure.
In drawing up the matrix to solve a system of linear equations as a unit of measurement to take a unknown. For example, a unit of the decimal number system (just a number, the constant term of the equation), x, y, z, XXL ... Oh! It not from here, this unit is used to measure blouses. By the way, if you write in a matrix the number of your blouses, the matrix of this does not hurt - it does not matter what or where you are writing. But the correct solution to a system of equations with the matrix in the blouse you have not come out.
The principle of a matrix of equations for you take the numerical coefficients before unknown and inscribe them each into the place. That is where the matter of what and where exactly do you fit into the matrix. Then the resulting matrix solving.
Where is yet used principle of mathematical operations with matrices? When you count a whole bunch of money in paper notes and coins. Laid out bills and coins into piles on the dignity and recalculate the number in each pile. On this matrix method ends, farther you bring the got results to a single unit of measurement. Naturally, performing similar actions in everyday life, we never think about how it can be described mathematically.
Remember, we talked about the meters and decimetres? About bows and flounces, on a multi-core processor? There also can be used matrix methods of addition and subtraction. Perform all actions with the same unit of measurement, then all of the other unit of measurement. In the end, if necessary, make conversion between different units of measurement to another.
This method is very good to use in geodesy, when you need to add or subtract a large number of angles in degrees, minutes, seconds. Doing all the actions in degrees, then a minute, then with seconds. And then all received converting seconds into minutes and seconds. To obtain the minute add or subtract those moments obtained after converting seconds. Convert the result to degrees and minutes. To add on the total number of degrees degrees of minutes. All you have turned a corner in degrees, minutes, seconds.
I hope this article will be useful in practice, and you're using methods of matrix computations is in full knowledge of what you are doing and what the result will get.
Sunday, August 26, 2012
Unsolvable equalizations are in preschool
The decision of unsolvable equalization caused some questions. Now we on the other hand will look at unsolvable equalization a number 1:
x + 2 = x
For this purpose we will create task research force and will nose after her behavior. In a research group we will plug:
1) Child from preschool. He only begins to understand the elements of mathematics but already considers well.
2) Blonde, mother of child from preschool. Once at school taught mathematics and knew it well. Now she forgot everything.
3) Professor of mathematics De Colletage. Brilliantly owns a mathematical vehicle, decides the most intricate mathematical problems.
4) Nikolay Khyzhnjak. Engineer, addicts to mathematics, asserts that understands this abstract science.
You will say that it is not honest, to include itself in the complement of research group. But, respected, I thought of this group, I offered candidates in her composition, I assert final composition of research group. It is the most democratic principle. I honestly took advantage of democratic right to be select and won in the competition of candidates :)))
And so, we will ask our research group to decide a simple task and give the algebraic variant of her decision:
We have an unknown amount of hedgehogs to that added two grass-snakes. How many hedgehogs did turn out?
As a result a research group gave out next decisions.
1) Child from preschool. As I talked already, a child is clever and able to decide logical tasks, in that it is needed to guess the train of thoughts of author of task and give the same answer that waits from a child author of task. It is such method of training of future zombis, that is well able to guess that is waited from them by owners. A child answered the unknown amount of hedgehogs" will "Turn out. On a request to write down the decision of this task on the sheet of paper, a child answered that to write he is not yet able, but can draw a hedgehog.
2) Blonde, mother of child from preschool. A blonde correctly decided a task after the row of leading questions. On a request to write down the decision through algebra, she began to reason: "Algebra, algebra... Nothing I remember... Algebra means - this unknown... Wow! We will designate the unknown amount of hedgehogs through "х". The amount of grass-snakes is known us and designating him is not needed, simply a number we write... Addition for us - it a sign "plus". Here"!. A blonde stretches out the sheet of paper, it is writtenin on that:
x + 2 = x
3) Professor of mathematics De Colletage. On a request to decide a task about hedgehogs and grass-snakes a famous professor was indignant, that it is ashamed to the great scientist to decide such child's tasks. He sent us after the decision of task in kindergarten. On our request to write down the algebraic decision of this task, a professor непонимающе looked at us, long thought and said: "Well, I will think above this problem". And was farther following...
For the algebraic reflection of decision of this task a professor worked out the special theory of three-cornered integrals, for that him was awarded with rank "academician". To the three-cornered integral the name of author was appropriated and he began to be named "Three-cornered integral De Colletage"...
For the decision of this concrete task the special research institute was created at the head with now already by an academician De Colletage. After a few years of the strained work, multivolume scientific work bore under the name "Practical application of three-cornered integral De Colletage in limits on the radius of cut on a dress"...
All of it nearscientific delirium we we will not study. We are interested only by a result. At once we open the last page of the last volume. There list of some organizations... We leaf pages to beginning of book in search of answer for a task... Somewhere in the middle of the last volume we find a line "Hired executed on account of working off scientific underbacks : .". Oho! This gang of easy riders from science on an even place managed to guzzle the whole lot of moneys! And before this line it is possible to find an answer for our task. "Х" is there written with plenty of reservations.
4) Nikolay Khyzhnjak. This witch-doctor of mathematics profoundly gave out a page under the name "Decision of unsolvable equalizations". According to his opinion, there is other task in that asked, how many hedgehogs will turn out, if to two hedgehogs to add the unknown amount of grass-snakes. He assures that both tasks have an identical decision :)))
By the way, there is another interesting task about grass-snakes and hedgehogs:
Mixture of grass-snake and hedgehog is a meter of the barbed wire. How mathematically to write down this expression?

Three-cornered integral De Colletage on the cut of dress not to apply :)))
x + 2 = x
For this purpose we will create task research force and will nose after her behavior. In a research group we will plug:
1) Child from preschool. He only begins to understand the elements of mathematics but already considers well.
2) Blonde, mother of child from preschool. Once at school taught mathematics and knew it well. Now she forgot everything.
3) Professor of mathematics De Colletage. Brilliantly owns a mathematical vehicle, decides the most intricate mathematical problems.
4) Nikolay Khyzhnjak. Engineer, addicts to mathematics, asserts that understands this abstract science.
You will say that it is not honest, to include itself in the complement of research group. But, respected, I thought of this group, I offered candidates in her composition, I assert final composition of research group. It is the most democratic principle. I honestly took advantage of democratic right to be select and won in the competition of candidates :)))
And so, we will ask our research group to decide a simple task and give the algebraic variant of her decision:
We have an unknown amount of hedgehogs to that added two grass-snakes. How many hedgehogs did turn out?
As a result a research group gave out next decisions.
1) Child from preschool. As I talked already, a child is clever and able to decide logical tasks, in that it is needed to guess the train of thoughts of author of task and give the same answer that waits from a child author of task. It is such method of training of future zombis, that is well able to guess that is waited from them by owners. A child answered the unknown amount of hedgehogs" will "Turn out. On a request to write down the decision of this task on the sheet of paper, a child answered that to write he is not yet able, but can draw a hedgehog.
2) Blonde, mother of child from preschool. A blonde correctly decided a task after the row of leading questions. On a request to write down the decision through algebra, she began to reason: "Algebra, algebra... Nothing I remember... Algebra means - this unknown... Wow! We will designate the unknown amount of hedgehogs through "х". The amount of grass-snakes is known us and designating him is not needed, simply a number we write... Addition for us - it a sign "plus". Here"!. A blonde stretches out the sheet of paper, it is writtenin on that:
x + 2 = x
3) Professor of mathematics De Colletage. On a request to decide a task about hedgehogs and grass-snakes a famous professor was indignant, that it is ashamed to the great scientist to decide such child's tasks. He sent us after the decision of task in kindergarten. On our request to write down the algebraic decision of this task, a professor непонимающе looked at us, long thought and said: "Well, I will think above this problem". And was farther following...
For the algebraic reflection of decision of this task a professor worked out the special theory of three-cornered integrals, for that him was awarded with rank "academician". To the three-cornered integral the name of author was appropriated and he began to be named "Three-cornered integral De Colletage"...
For the decision of this concrete task the special research institute was created at the head with now already by an academician De Colletage. After a few years of the strained work, multivolume scientific work bore under the name "Practical application of three-cornered integral De Colletage in limits on the radius of cut on a dress"...
All of it nearscientific delirium we we will not study. We are interested only by a result. At once we open the last page of the last volume. There list of some organizations... We leaf pages to beginning of book in search of answer for a task... Somewhere in the middle of the last volume we find a line "Hired executed on account of working off scientific underbacks : .". Oho! This gang of easy riders from science on an even place managed to guzzle the whole lot of moneys! And before this line it is possible to find an answer for our task. "Х" is there written with plenty of reservations.
4) Nikolay Khyzhnjak. This witch-doctor of mathematics profoundly gave out a page under the name "Decision of unsolvable equalizations". According to his opinion, there is other task in that asked, how many hedgehogs will turn out, if to two hedgehogs to add the unknown amount of grass-snakes. He assures that both tasks have an identical decision :)))
By the way, there is another interesting task about grass-snakes and hedgehogs:
Mixture of grass-snake and hedgehog is a meter of the barbed wire. How mathematically to write down this expression?

Three-cornered integral De Colletage on the cut of dress not to apply :)))
Sunday, August 19, 2012
Complex numbers
Complex numbers we we will not examine now with you. If you need to understand complex numbers, take textbooks, swarm in the Internet - information is enough there. I now do not want to engage in complex numbers.
If you want to know my personal opinion about complex numbers, then I will say that all of it is nonsense. On one mathematical forum I read a request about the help of some physicist. He writes there, that he succeeded to decide some equations in an eightmeasure complex space. Now he had a question, as got decision from an eightmeasure complex space to translate in ordinary space. Was it so desirable to say him: "And what fool compels you to decide it in complex space? Do not climb in complex spaces, and you will not have to return back"!
For me the weightiest argument in behalf on fabulosity of complex numbers is circumstance that in all history of existence of complex numbers not a single mathematician got the salary in complex numbers.
I consider that complex numbers are a first-ever virtual game for adults. Game it so pleased all, that in her with enthusiasm play until now. If to look at complex numbers from the point of view of Code of criminal procedure, then this will be an usual swindle. Сomplex numbers can be named a scale swindle in history of science. Notice, we thought of a rule about that, whatever ignorance of law releases from responsibility. I will add from itself, that the laws of mathematics I do not consider an exception. "One law for all" - is mathematics. "One law for all, except me and I will say, to whom the action of law does not spread yet" - it all other.
Due to existence of complex numbers in that nobody understands nothing, mathematicians occupy the same position today, what in ancient times was occupied by priests. Only mathematicians are known all secrets of complex numbers and only mathematicians know that it is needed to do with these complex numbers.
The not last role in development of imaginaries was played by the bureaucratic system. When nobody of simple people understands nothing, they can talk whatever. So hypercomplex numbers appeared. If you want to succeed in the bureaucratic system, then imaginaries for you are the real treasure. You easily can think of some super-puper-bam-trah-plus hypercomplex number. Thus every new prefix to the complex numbers gives an opportunity to write practically an infinite amount to nobody not clear dissertations and to get for it real, but not complex, money. Then you to the pension will teach other that in what understand nothing. All very simply. An even talking parrot can be taught to pronounce mathematical determinations. Any train animal is able to execute certain actions in a certain sequence. People yield to training much better of any animal, therefore they handle complex numbers so adroitly.
Complex numbers are an example that can turn out, if problem to decide not correctly. Those problems that mathematicians decide in relative stem of coordinates with the use of complex numbers must decide in the absolute system of coordinates, where complex numbers can not arise up in principle, as there are not negative numbers from that it was possible to extract a root square and to get an complex number. Search these decisions and you them will find necessarily. Transport companies perfectly managed with the decision of similar problem, in a difference from mathematicians. Whatever direction you went in, in direct or reverse, you always pay and never pay to you, even if you countermarch. I think that in the future expression "complex numbers" will be used approximately in the same sense, in what we today apply expression "three whale". For example, if a student will go out to the board and will say "I can not decide" it, a teacher him will advise "You enter complex numbers".
We will look now, where complex numbers appeared from. Show to me those real circumstances mathematical description of that results in appearance of equation
x² + 1 = 0
I can dream up. We it admits, someone printed great symbols on the sheet of paper equation in that a sign costs minus. With this sheet he went for a walk on a zoo and by chance dropped a sheet check to the monkey. A monkey heaved up this sheet, conducted on it the dirty finger. On a clean chance this dirty finger converted a sign minus in a sign plus. A monkey looked on the got result, thought: "Nonsense some, in jungles such equations are not" and threw out this sheet from a cage. At this time by a cage with a monkey a mathematician passed and picked up an ill-starred sheet. "What interesting equation" - a mathematician thought and began him to decide. Imaginaries appeared as a result of decision. Told a story fully applies on realisticness, but to mathematics she has no relation.
Think, I clear enough expounded the point of view on complex numbers. I hope, nobody of believing in existence complex numbers will begin to consider this article as insult of feelings of believers. You can believe in whatever: in God, in Devil or in complex numbers. But it is not necessary to compel me to believe in the same.
That to do to you, did eat you compel to teach complex numbers? Teach - such are bureaucratic rules of playing education. Do you want to get the scrap of paper, confirmative, that for you clever brain on shoulders? Here when you will take the deserving place in the bureaucratic system of science or education, then will decide, continue these playing complex numbers or give up them.
If you want to know my personal opinion about complex numbers, then I will say that all of it is nonsense. On one mathematical forum I read a request about the help of some physicist. He writes there, that he succeeded to decide some equations in an eightmeasure complex space. Now he had a question, as got decision from an eightmeasure complex space to translate in ordinary space. Was it so desirable to say him: "And what fool compels you to decide it in complex space? Do not climb in complex spaces, and you will not have to return back"!
For me the weightiest argument in behalf on fabulosity of complex numbers is circumstance that in all history of existence of complex numbers not a single mathematician got the salary in complex numbers.
I consider that complex numbers are a first-ever virtual game for adults. Game it so pleased all, that in her with enthusiasm play until now. If to look at complex numbers from the point of view of Code of criminal procedure, then this will be an usual swindle. Сomplex numbers can be named a scale swindle in history of science. Notice, we thought of a rule about that, whatever ignorance of law releases from responsibility. I will add from itself, that the laws of mathematics I do not consider an exception. "One law for all" - is mathematics. "One law for all, except me and I will say, to whom the action of law does not spread yet" - it all other.
Due to existence of complex numbers in that nobody understands nothing, mathematicians occupy the same position today, what in ancient times was occupied by priests. Only mathematicians are known all secrets of complex numbers and only mathematicians know that it is needed to do with these complex numbers.
The not last role in development of imaginaries was played by the bureaucratic system. When nobody of simple people understands nothing, they can talk whatever. So hypercomplex numbers appeared. If you want to succeed in the bureaucratic system, then imaginaries for you are the real treasure. You easily can think of some super-puper-bam-trah-plus hypercomplex number. Thus every new prefix to the complex numbers gives an opportunity to write practically an infinite amount to nobody not clear dissertations and to get for it real, but not complex, money. Then you to the pension will teach other that in what understand nothing. All very simply. An even talking parrot can be taught to pronounce mathematical determinations. Any train animal is able to execute certain actions in a certain sequence. People yield to training much better of any animal, therefore they handle complex numbers so adroitly.
Complex numbers are an example that can turn out, if problem to decide not correctly. Those problems that mathematicians decide in relative stem of coordinates with the use of complex numbers must decide in the absolute system of coordinates, where complex numbers can not arise up in principle, as there are not negative numbers from that it was possible to extract a root square and to get an complex number. Search these decisions and you them will find necessarily. Transport companies perfectly managed with the decision of similar problem, in a difference from mathematicians. Whatever direction you went in, in direct or reverse, you always pay and never pay to you, even if you countermarch. I think that in the future expression "complex numbers" will be used approximately in the same sense, in what we today apply expression "three whale". For example, if a student will go out to the board and will say "I can not decide" it, a teacher him will advise "You enter complex numbers".
We will look now, where complex numbers appeared from. Show to me those real circumstances mathematical description of that results in appearance of equation
x² + 1 = 0
I can dream up. We it admits, someone printed great symbols on the sheet of paper equation in that a sign costs minus. With this sheet he went for a walk on a zoo and by chance dropped a sheet check to the monkey. A monkey heaved up this sheet, conducted on it the dirty finger. On a clean chance this dirty finger converted a sign minus in a sign plus. A monkey looked on the got result, thought: "Nonsense some, in jungles such equations are not" and threw out this sheet from a cage. At this time by a cage with a monkey a mathematician passed and picked up an ill-starred sheet. "What interesting equation" - a mathematician thought and began him to decide. Imaginaries appeared as a result of decision. Told a story fully applies on realisticness, but to mathematics she has no relation.
Think, I clear enough expounded the point of view on complex numbers. I hope, nobody of believing in existence complex numbers will begin to consider this article as insult of feelings of believers. You can believe in whatever: in God, in Devil or in complex numbers. But it is not necessary to compel me to believe in the same.
That to do to you, did eat you compel to teach complex numbers? Teach - such are bureaucratic rules of playing education. Do you want to get the scrap of paper, confirmative, that for you clever brain on shoulders? Here when you will take the deserving place in the bureaucratic system of science or education, then will decide, continue these playing complex numbers or give up them.
Wednesday, August 15, 2012
Decision of unsolvable equations
In comments to the article infant "Wunderkindes and cretin with blondes" (in Russian language) me offered to decide a few equations it is "known from a digit, that a decision is not present". These equations look like the following:
1) x + 2 = x
2) √x = -1
3) x/0 = x
Probably, on mathematicians these unsolvable equations operate, as a boa on rabbit and infuse with in their souls the awesome trembling. I am deprived such superstitions. Moreover, the author of this idea, Vag, tossed up to me a magic stick:
"Decisions does not have" means that it is WELL-PROVEN that such circumstances at that problem abode by ARE not.
Today we will consider circumstances at that terms at least one of equations observed. Consequently, at least one unsolvable equation we will decide now.
But to begin would I like not from a decision, and from an answer to the question: "Where these unsolvable equations appeared from?" Me it seems to, here from where...
...A mother bought to the child a new toy are blocks with an alphabet. She collected a few words from blocks, read them and gave blocks to the child. A mother took up the everyday businesses.

A child with enthusiasm began to fold blocks. Finishing to lay out series from the blocks taken by chance, he put question to the mother:
- That is here written?
- Nothing. You laid down letters wrong, - a mother explained, - When will learn letters, then you will be able correctly to fold blocks.
A child was very offended and burst into tears. What a more mother tried to quiet him, the he cried stronger. Then a mother said:
- Well, try once again, I necessarily will read you.
Bustling a nose, a child at random took a few blocks and laid down them in series.
- What did I write? - he asked with tears.
Farther not to disorder a child, a mother answered:
- In mathematics a certain integral is so designated in limits from Old Testament to nine evening, taken on the surface of asynchronous point.
A child quieted down puzzled. He understood nothing, but something disturbed him in this phrase. A bit thinking, he asked:
- And will a fairy-tale be at nine o'clock of evening?
- It will be necessarily. Where will she go? - a mother answered very confidently.
Very attentively looking to the mother in eyes, a child by touch took a few blocks and laid down another abracadabra.
- And it what did I write? - he asked with distrust, not tearing away a look from mother eyes.
If a mother will not look at blocks will say that is written there, she means cheats him. If will look - she means that is written there really reads.
A mother looked another portion of incoherent words at blocks and crfpfkf. A child was happy. He has the most clever mother! Farther this game proceeded until child not tired of. He really had a clever mother that knew many clever words.
A child grew up then, learned letters, began independently to fold words from blocks. When he became adult, he forgot playing blocks, but faith that for him the most clever mother, remained...
Just as a child made blocks, mathematicians worked out unsolvable equations from mathematical symbols. A child grew and became adult, mathematicians so remained in pampers of the determinations.
Now we will pass to business.
Decision of the first unsolvable equation
x + 2 = x
This equation traditionally can be taken to next equality
2 = 0
As this equality did not look wildly, but in mathematics such quite possible. I will say anymore, the first equation is only one equation from the system of two equations, that has one common decision. The second equation looks so:
2 + х = 2
This equation is usually taken to equality
х = 0
The decision of this system of equations looks so:
х ⊥ 2
It means that the numbers taken by you are on perpendicular numerical axes, therefore the rules of ordinary arithmetic give such result.

I especially want to underline that all the known rule "from transposition of elements a sum does not change" in this case stops to work. A result depends on that, what number you take for basis at implementation of action of addition.
The further decision of this system of equalizations is possible two methods resulting in different results.
First method. Turn of one of numerical axes on 90 degrees and passing to the rules of ordinary addition. Undeniable equality will ensue:
x + 2 = x + 2
In this case the laws of symmetry of mathematical actions begin to work.
Second method. Remaining in the rectangular system of coordinates, to apply the methods of vectorial algebra and find a sum on the theorem of Pythagoras, where х and 2 are the cathetuses of rectangular triangle, and result of addition - by a hypotenuse. If you consider that application of facilities of vectorial algebra is impossible, when on the ends of sticks the tips of pointers are absent, then it is your personal problems already. In this case both equalizations of the system are taken to the identical decision:
x + 2 = √(x² + 2²)
It is done away with the decision of this unsolvable equalization. you need to be only determined with the desires - what result needs you.
Decision of the second unsolvable equalization.
√x = -1
This decision caused most difficulties from the simplicity. We erect both parts of equalization in a square and get an answer:
x = 1
This equalization is taken to equality:
+1 = -1
In the parallel instances of mathematics usually begin to dissert upon the modules of numbers. I will say that before to put signs before numbers, it is needed to understand sense of positive and negative numbers.
Decision of the third unsolvable equalization
x/0 = x
The decision of this equalization is taken to equality:
1 = 0
Personally for me there is nothing unusual in this equality. This one of basic equalities of mathematics, without that mathematics in principle is impossible. If our mathematicians until now do without this equality, then only due to the pampers. At exposition of mathematics on the pages of this web-site I will repeatedly call to this equality.
To accept the solutions offered by me or not accept is this your personal file. Monkeys too nobody compelled to go down on earth. Many of them until now on branches bruise along and fully happy without pampers))))
1) x + 2 = x
2) √x = -1
3) x/0 = x
Probably, on mathematicians these unsolvable equations operate, as a boa on rabbit and infuse with in their souls the awesome trembling. I am deprived such superstitions. Moreover, the author of this idea, Vag, tossed up to me a magic stick:
"Decisions does not have" means that it is WELL-PROVEN that such circumstances at that problem abode by ARE not.
Today we will consider circumstances at that terms at least one of equations observed. Consequently, at least one unsolvable equation we will decide now.
But to begin would I like not from a decision, and from an answer to the question: "Where these unsolvable equations appeared from?" Me it seems to, here from where...
...A mother bought to the child a new toy are blocks with an alphabet. She collected a few words from blocks, read them and gave blocks to the child. A mother took up the everyday businesses.

A child with enthusiasm began to fold blocks. Finishing to lay out series from the blocks taken by chance, he put question to the mother:
- That is here written?
- Nothing. You laid down letters wrong, - a mother explained, - When will learn letters, then you will be able correctly to fold blocks.
A child was very offended and burst into tears. What a more mother tried to quiet him, the he cried stronger. Then a mother said:
- Well, try once again, I necessarily will read you.
Bustling a nose, a child at random took a few blocks and laid down them in series.
- What did I write? - he asked with tears.
Farther not to disorder a child, a mother answered:
- In mathematics a certain integral is so designated in limits from Old Testament to nine evening, taken on the surface of asynchronous point.
A child quieted down puzzled. He understood nothing, but something disturbed him in this phrase. A bit thinking, he asked:
- And will a fairy-tale be at nine o'clock of evening?
- It will be necessarily. Where will she go? - a mother answered very confidently.
Very attentively looking to the mother in eyes, a child by touch took a few blocks and laid down another abracadabra.
- And it what did I write? - he asked with distrust, not tearing away a look from mother eyes.
If a mother will not look at blocks will say that is written there, she means cheats him. If will look - she means that is written there really reads.
A mother looked another portion of incoherent words at blocks and crfpfkf. A child was happy. He has the most clever mother! Farther this game proceeded until child not tired of. He really had a clever mother that knew many clever words.
A child grew up then, learned letters, began independently to fold words from blocks. When he became adult, he forgot playing blocks, but faith that for him the most clever mother, remained...
Just as a child made blocks, mathematicians worked out unsolvable equations from mathematical symbols. A child grew and became adult, mathematicians so remained in pampers of the determinations.
Now we will pass to business.
Decision of the first unsolvable equation
x + 2 = x
This equation traditionally can be taken to next equality
2 = 0
As this equality did not look wildly, but in mathematics such quite possible. I will say anymore, the first equation is only one equation from the system of two equations, that has one common decision. The second equation looks so:
2 + х = 2
This equation is usually taken to equality
х = 0
The decision of this system of equations looks so:
х ⊥ 2
It means that the numbers taken by you are on perpendicular numerical axes, therefore the rules of ordinary arithmetic give such result.

I especially want to underline that all the known rule "from transposition of elements a sum does not change" in this case stops to work. A result depends on that, what number you take for basis at implementation of action of addition.
The further decision of this system of equalizations is possible two methods resulting in different results.
First method. Turn of one of numerical axes on 90 degrees and passing to the rules of ordinary addition. Undeniable equality will ensue:
x + 2 = x + 2
In this case the laws of symmetry of mathematical actions begin to work.
Second method. Remaining in the rectangular system of coordinates, to apply the methods of vectorial algebra and find a sum on the theorem of Pythagoras, where х and 2 are the cathetuses of rectangular triangle, and result of addition - by a hypotenuse. If you consider that application of facilities of vectorial algebra is impossible, when on the ends of sticks the tips of pointers are absent, then it is your personal problems already. In this case both equalizations of the system are taken to the identical decision:
x + 2 = √(x² + 2²)
It is done away with the decision of this unsolvable equalization. you need to be only determined with the desires - what result needs you.
Decision of the second unsolvable equalization.
√x = -1
This decision caused most difficulties from the simplicity. We erect both parts of equalization in a square and get an answer:
x = 1
This equalization is taken to equality:
+1 = -1
In the parallel instances of mathematics usually begin to dissert upon the modules of numbers. I will say that before to put signs before numbers, it is needed to understand sense of positive and negative numbers.
Decision of the third unsolvable equalization
x/0 = x
The decision of this equalization is taken to equality:
1 = 0
Personally for me there is nothing unusual in this equality. This one of basic equalities of mathematics, without that mathematics in principle is impossible. If our mathematicians until now do without this equality, then only due to the pampers. At exposition of mathematics on the pages of this web-site I will repeatedly call to this equality.
To accept the solutions offered by me or not accept is this your personal file. Monkeys too nobody compelled to go down on earth. Many of them until now on branches bruise along and fully happy without pampers))))
Theorem about parallel lines, thought of in motion
While I wrote about the types of triangles, I was visited by one idea - I thought of a theorem about parallel lines. She sounds so:
distance between parallel lines (by planes, volumes etc.) it is impossible to define mathematical methods
To engage in proof of this theorem about parallel lines we will not be now with you. We will leave proof on the future. If are wishing to prove or refute this theorem - occupy.
You can argue that there are very much tasks in the textbooks of mathematics, where it is needed to find distance between parallel lines and all of them decide mathematical methods. I agree, but... In the textbooks of mathematics I am much such, what is not present in mathematics. Yet more in mathematics what is not present in the textbooks of mathematics. Little by little we will understand with you, who is who in mathematics and where it undertakes from. And we will begin from unsolvable equalizations.
More interesting things on the page "New Math".
distance between parallel lines (by planes, volumes etc.) it is impossible to define mathematical methods
To engage in proof of this theorem about parallel lines we will not be now with you. We will leave proof on the future. If are wishing to prove or refute this theorem - occupy.
You can argue that there are very much tasks in the textbooks of mathematics, where it is needed to find distance between parallel lines and all of them decide mathematical methods. I agree, but... In the textbooks of mathematics I am much such, what is not present in mathematics. Yet more in mathematics what is not present in the textbooks of mathematics. Little by little we will understand with you, who is who in mathematics and where it undertakes from. And we will begin from unsolvable equalizations.
More interesting things on the page "New Math".
Sunday, July 08, 2012
What trigonometric circle?
What trigonometric circle? Yet he is named trigonometric circumference. Question interesting enough. We will not go into the details of distinctions of concepts "circle" and "circumference". Although, for blondes I will explain that a circle is a coin or hole from a bagel, a circumference is this wedding ring or bagel. Coming from classic determination of trigonometric functions, more correct to talk "trigonometric circumference", as the question is about the set of points and their coordinates, but not about a flat figure and her area. But in the Internet much more often search a "trigonometric circle" exactly, probably because collecting so less letters is necessary.
Before we will pass to formulation of determinations of trigonometric functions with the use of portrait of tangent, we need to understand, what a trigonometric circle differs from all other circles. In reasoning we will use one mathematical focus sense of that is based exactly on these differences.
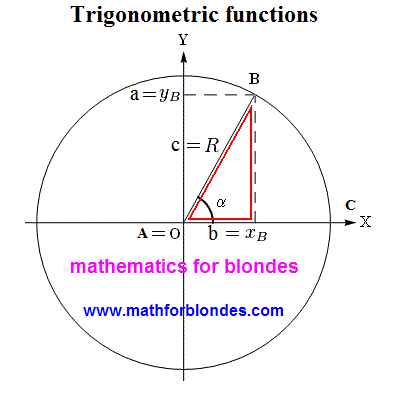
We will take the picture of circumference from determination of trigonometric functions. He looks here so.

On a picture the ordinary circumference of arbitrary radius is represented. As in the center of circumference cheekily fell to pieces the cartesian coordinate system, then all points of this circumference have vertical and horizontal coordinates. Radius of circumference and coordinate of points expressed by numbers. The intersections of axes of coordinates and circumference are determined by the size of radius of circumference and numeral him equal to.
In an order to convert an ordinary circumference into trigonometric one, it is needed to divide all elements of circumference into the radius of circumference. Letters of "X" and "Y" are the tags of the system of coordinates, designating her obtrusive presence on our picture. These letters by a radius are not divided, as well as letter of "B", designating a point on a circumference. Point "0"(zero) as a result of dividing by a radius so will remain a point "0"(remember, the zero divided by any number equals a zero?). Corner alpha it is possible to divide into a number, but it is impossible to divide into a radius circumferences(by the way, here to you the prepared proof that a division does not make sense) :))), therefore a corner it is better not to touch, in order to avoid large troubles(from all present person on a picture, a corner is the steepest element, he is in all trigonometric functions in the natural kind). For us remain only radius of circumference and coordinate points of "B", that we can divide into the size of radius of circumference.
Clear that at dividing of radius of circumference by an exactly such radius, we will get unit as a result. And at dividing of coordinates of point of circumference by a radius we will get the values of sine and cosine of corner alpha(on determination of trigonometric functions). That is our transformations look on a picture.

Now we need only to substitute all radiuses by units and coordinates of point on a sine and cosine of corner alpha and a trigonometric circumference will turn out for us. We even can set forth determination of single circumference (let child prodigy teach):
a circumference with a radius equal to unit is named a trigonometric circumference, if there is a center of the cartesian system of coordinates in the center of circumference.
This determination far not complete and does not take into account many nuances on that mathematicians take no notice usually. But about it we better will talk at the study of properties of trigonometric functions. And while we will look at a picture, as a trigonometric circumference looks in all beauty.
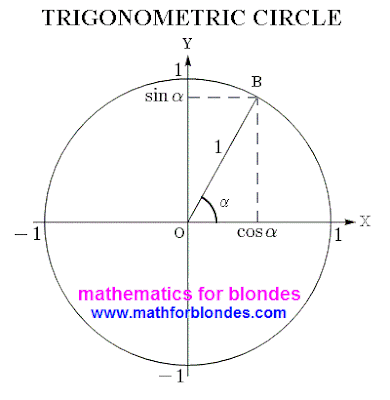
Actually, this is a trigonometric circle. If on him to place the values of different corners and corresponding to them values of sine and cosine, then we will get the trigonometric circle of sine and cosine.
Now about that focus that we will do during formulation of determinations of trigonometric functions. Here we substituted the radius of circumference by unit, and there we will act vice versa - we will replace unit the radius of circumference. Id est, from a trigonometric circumference to pass to the circumference of arbitrary radius, as that is required by a textbook on mathematics.
Before we will pass to formulation of determinations of trigonometric functions with the use of portrait of tangent, we need to understand, what a trigonometric circle differs from all other circles. In reasoning we will use one mathematical focus sense of that is based exactly on these differences.
We will take the picture of circumference from determination of trigonometric functions. He looks here so.

On a picture the ordinary circumference of arbitrary radius is represented. As in the center of circumference cheekily fell to pieces the cartesian coordinate system, then all points of this circumference have vertical and horizontal coordinates. Radius of circumference and coordinate of points expressed by numbers. The intersections of axes of coordinates and circumference are determined by the size of radius of circumference and numeral him equal to.
In an order to convert an ordinary circumference into trigonometric one, it is needed to divide all elements of circumference into the radius of circumference. Letters of "X" and "Y" are the tags of the system of coordinates, designating her obtrusive presence on our picture. These letters by a radius are not divided, as well as letter of "B", designating a point on a circumference. Point "0"(zero) as a result of dividing by a radius so will remain a point "0"(remember, the zero divided by any number equals a zero?). Corner alpha it is possible to divide into a number, but it is impossible to divide into a radius circumferences(by the way, here to you the prepared proof that a division does not make sense) :))), therefore a corner it is better not to touch, in order to avoid large troubles(from all present person on a picture, a corner is the steepest element, he is in all trigonometric functions in the natural kind). For us remain only radius of circumference and coordinate points of "B", that we can divide into the size of radius of circumference.
Clear that at dividing of radius of circumference by an exactly such radius, we will get unit as a result. And at dividing of coordinates of point of circumference by a radius we will get the values of sine and cosine of corner alpha(on determination of trigonometric functions). That is our transformations look on a picture.

Now we need only to substitute all radiuses by units and coordinates of point on a sine and cosine of corner alpha and a trigonometric circumference will turn out for us. We even can set forth determination of single circumference (let child prodigy teach):
a circumference with a radius equal to unit is named a trigonometric circumference, if there is a center of the cartesian system of coordinates in the center of circumference.
This determination far not complete and does not take into account many nuances on that mathematicians take no notice usually. But about it we better will talk at the study of properties of trigonometric functions. And while we will look at a picture, as a trigonometric circumference looks in all beauty.

Actually, this is a trigonometric circle. If on him to place the values of different corners and corresponding to them values of sine and cosine, then we will get the trigonometric circle of sine and cosine.
Now about that focus that we will do during formulation of determinations of trigonometric functions. Here we substituted the radius of circumference by unit, and there we will act vice versa - we will replace unit the radius of circumference. Id est, from a trigonometric circumference to pass to the circumference of arbitrary radius, as that is required by a textbook on mathematics.
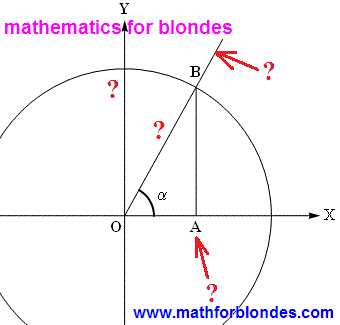
Trigonometric functions determination through a triangle
Trigonometric functions can be determined on a rectangular triangle. On a picture you can see determinations of all trigonometric functions through the elements of rectangular triangle.

It is another icon for hanging out on a wall and overlearnings of text. We this we will not engage in. We will look better, as possible to combine a rectangular triangle and circumference. For this purpose we will combine two pictures: circumference from classic determination of trigonometric functions and our triangle. We will place a triangle next to a circumference. That is it looks.
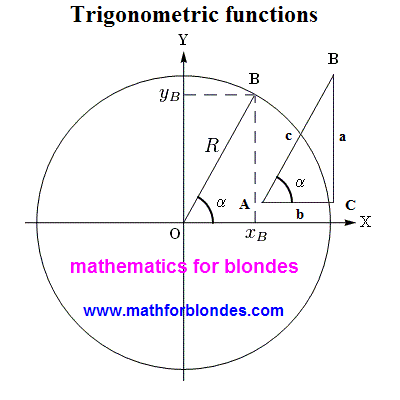
As see, pictures are practically identical, and component elements are named differently in them. Identically mark only corner alpha and point of "B". Now we will impose a triangle straight on a circumference. All graphic images accepted for a circumference we will save, and a rectangular triangle we will underline red lines on the inside (type we will lead around the contour of triangle lipstick).
As be obvious from a picture, the hypotenuse of rectangular triangle grows into the radius of circumference, cathetuses become equal to the coordinates of point. It as in a human language - a the same concept in different languages is designated by different words. This distinction in a pronunciation does not give to us to understand foreign languages. Approximately the same takes place in mathematics. Some consider determination of trigonometric functions on a rectangular triangle primitive. If you want to understand mathematics, will memorize the following: there are not primitive things in mathematics. There are primitive creatures counting itself very clever. Exactly desire to seem more clever than other, resulted in that mathematicians almost nothing is understood in mathematics.
Specially I will quote a phrase from Russian-language Wikipedia, where talked about determination of trigonometric functions on a triangle: "This determination has some pedagogical advantage, because does not require introductions of concept of the system of coordinates, but also such large defect, that it is impossible to define trigonometric functions even for obtuse angles that must be known at the decision of elementary tasks about amblygons". Honestly speaking, like thick ignorance of mathematicians simply shocks me. What triangle are trigonometric functions determined for? Correctly, for RECTANGULAR. Let though one mathematician will show to me RECTANGULAR TRIANGLE With OBTUSE ANGLE. I swear to you, as soon as I will see this geometrical miracle, I here will invert the portrait of tangent heels over head and I will hang oneself on a cosine. Not a single mathematician understands really, that the decision of "elementary tasks about amblygons" through trigonometric functions is ALWAYS taken to breaking up of one amblygon on two rectangular triangles?
Now I will show the most primitive example of existence of trigonometry you in life. More primitive, probably, is not already.

Look at a photo - how many human bodies serenely stationed oneself on the horizontal plane of rock, at the same time there is nobody on a vertical plane. Why? And because trigonometric functions for perpendicular direction have quite another values. For us with you basic sense of trigonometric functions is that exactly trigonometric functions determine our possibilities.

It is another icon for hanging out on a wall and overlearnings of text. We this we will not engage in. We will look better, as possible to combine a rectangular triangle and circumference. For this purpose we will combine two pictures: circumference from classic determination of trigonometric functions and our triangle. We will place a triangle next to a circumference. That is it looks.

As see, pictures are practically identical, and component elements are named differently in them. Identically mark only corner alpha and point of "B". Now we will impose a triangle straight on a circumference. All graphic images accepted for a circumference we will save, and a rectangular triangle we will underline red lines on the inside (type we will lead around the contour of triangle lipstick).

As be obvious from a picture, the hypotenuse of rectangular triangle grows into the radius of circumference, cathetuses become equal to the coordinates of point. It as in a human language - a the same concept in different languages is designated by different words. This distinction in a pronunciation does not give to us to understand foreign languages. Approximately the same takes place in mathematics. Some consider determination of trigonometric functions on a rectangular triangle primitive. If you want to understand mathematics, will memorize the following: there are not primitive things in mathematics. There are primitive creatures counting itself very clever. Exactly desire to seem more clever than other, resulted in that mathematicians almost nothing is understood in mathematics.
Specially I will quote a phrase from Russian-language Wikipedia, where talked about determination of trigonometric functions on a triangle: "This determination has some pedagogical advantage, because does not require introductions of concept of the system of coordinates, but also such large defect, that it is impossible to define trigonometric functions even for obtuse angles that must be known at the decision of elementary tasks about amblygons". Honestly speaking, like thick ignorance of mathematicians simply shocks me. What triangle are trigonometric functions determined for? Correctly, for RECTANGULAR. Let though one mathematician will show to me RECTANGULAR TRIANGLE With OBTUSE ANGLE. I swear to you, as soon as I will see this geometrical miracle, I here will invert the portrait of tangent heels over head and I will hang oneself on a cosine. Not a single mathematician understands really, that the decision of "elementary tasks about amblygons" through trigonometric functions is ALWAYS taken to breaking up of one amblygon on two rectangular triangles?
Now I will show the most primitive example of existence of trigonometry you in life. More primitive, probably, is not already.

Look at a photo - how many human bodies serenely stationed oneself on the horizontal plane of rock, at the same time there is nobody on a vertical plane. Why? And because trigonometric functions for perpendicular direction have quite another values. For us with you basic sense of trigonometric functions is that exactly trigonometric functions determine our possibilities.
Tuesday, July 03, 2012
Trigonometric functions are determination
Determination of trigonometric functions I took from Russian-language part of Wikipedia and designed as a picture. You can look and read.

Picture, naturally, I a bit did. In Wikipedia text of determination of trigonometric functions is written about one - about the coordinates of point and radius of circumference, and on a picture quite another is drawn. Probably, an artist from Wikipedia looked not in the that page of textbook on mathematics. Well yet, that he the textbook of mathematics with a textbook on biology did not entangle. Here that turned out for him.
Many of you can say: "I do not understand trigonometry. That to do"? Do the same, that do all mathematicians - bluntly teach determinations and, if necessary, pronounce them aloud, as talking parrots. For this purpose unseal my picture, hang up it above a bed and every evening before a dream read determination of trigonometric functions instead of prayer. I will open to you one great secret of mathematicians : those, who rewrites the determination given above from a textbook in a textbook, very small understand in mathematics in general, and quite nothing is understood in trigonometric functions in particular. Those, who understands, what trigonometric functions and able to use them, on all Universe travel in flying piattis. We hardly tear away the priests from a terrene through airplanes and rockets. By the way, would you like to exchange it stinking petrol car on an elegant flying object of UFO type?
If did you already read my notes How to memorize trigonometric functions? and the Trigonometric functions, then to you teaching nothing is not necessary. All, that it is needed for formulation of any determination of trigonometric functions, you know already. Later I will show you, as to use these knowledge. And while we will keep reading Wikipedia, where talked about determination of trigonometric functions for a rectangular triangle.

Picture, naturally, I a bit did. In Wikipedia text of determination of trigonometric functions is written about one - about the coordinates of point and radius of circumference, and on a picture quite another is drawn. Probably, an artist from Wikipedia looked not in the that page of textbook on mathematics. Well yet, that he the textbook of mathematics with a textbook on biology did not entangle. Here that turned out for him.

Many of you can say: "I do not understand trigonometry. That to do"? Do the same, that do all mathematicians - bluntly teach determinations and, if necessary, pronounce them aloud, as talking parrots. For this purpose unseal my picture, hang up it above a bed and every evening before a dream read determination of trigonometric functions instead of prayer. I will open to you one great secret of mathematicians : those, who rewrites the determination given above from a textbook in a textbook, very small understand in mathematics in general, and quite nothing is understood in trigonometric functions in particular. Those, who understands, what trigonometric functions and able to use them, on all Universe travel in flying piattis. We hardly tear away the priests from a terrene through airplanes and rockets. By the way, would you like to exchange it stinking petrol car on an elegant flying object of UFO type?
If did you already read my notes How to memorize trigonometric functions? and the Trigonometric functions, then to you teaching nothing is not necessary. All, that it is needed for formulation of any determination of trigonometric functions, you know already. Later I will show you, as to use these knowledge. And while we will keep reading Wikipedia, where talked about determination of trigonometric functions for a rectangular triangle.
Monday, July 02, 2012
Trigonometric functions
Trigonometric functions is simply. At the last time we considered the portrait of tangent, today we will expose the secrets of practical application of this masterpiece of painting.
Any trigonometric function is the result of division. It needs to be memorized forever. We divide something by something and as a result get a trigonometric function. That on what divided in trigonometric functions? Variants are different here. I suggest not to learn by rote you on memory all, in respect of trigonometric functions. Let us try simply to apply the portrait of tangent and minimum set of necessary knowledge.
And so, a tangent is a sine on a cosine. As we said hardly higher, in a tangent a sine is divided by a cosine. A division in mathematics can mark a fractional line or two points. We will transform our portrait of tangent in the record of partaking with two points. Here that turned out for us.

Most important, what we are taught by this picture, so it to those places, where it is needed to search sines and cosines. In the system of denotations accepted by mathematicians, sines always are situated on a vertical line - it upwards-downward. Cosines always are situated on a horizontal - it to the left-right (or aside). That is a complete set will look from 6 trigonometric functions in our variant of denotations. For evidentness a sine and cosine are depicted by a different color and we will add fractional hyphens wherein without them not to do.


Do not be frightened such amount of pictures. That it is represented in overhead part, above a red line, we almost learned already. We will repeat:
a sine - it upwards
Do you see? The half of trigonometric functions we learned already. With the second half, that under a red line, yet simpler - invert that you learned already heels over head. Remaining trigonometric functions are shots reverse already known to us. We swap a numerator and denominator - all is ready already for us.
With a cotangent all is simple. A cotangent is this attitude of cosine toward a sine. With gimbleting of tangent no problems arise up - he has both a numerator and denominator. But as to be with a sine and cosine? We do not have denominators of these shots in fact! Do not worry, any number has a denominator that in mathematics, writing is not accepted is unit. In a secant and cosecant exactly this unit appears in a numerator, and a cosine and sine are written in a denominator.
It is important to memorize! In the pairs of the names of trigonometric functions a secant is a cosine and cosecant - a sine can be only one prefix to on two names. If we take a sine for basis, then a reverse shot will be named cosecant. If we take a cosine, then a reverse shot is named secant, because one prefix to we already used up on a cosine.
It is important to memorize! In the pairs of the names of trigonometric functions a secant - is a cosine and cosecant - a sine can be only one prefix co on two names. If we take a sine for basis, then a reverse shot will be named cosecant. If we take a cosine, then a reverse shot is named secant, because one prefix co we already used up on a cosine.
In principle, it fully sufficiently, in determinations of trigonometric functions to feel, close as an oyster in water. A question remains not found out, that at a sine and cosine to write in a denominator instead of unit. In fact we said in beginning, that trigonometric functions are a result of division(relation) or shot. Do not worry, mathematicians will prompt us, that exactly they want there to see. For this purpose there are determinations of trigonometric functions. We will talk next time about them.
Any trigonometric function is the result of division. It needs to be memorized forever. We divide something by something and as a result get a trigonometric function. That on what divided in trigonometric functions? Variants are different here. I suggest not to learn by rote you on memory all, in respect of trigonometric functions. Let us try simply to apply the portrait of tangent and minimum set of necessary knowledge.
And so, a tangent is a sine on a cosine. As we said hardly higher, in a tangent a sine is divided by a cosine. A division in mathematics can mark a fractional line or two points. We will transform our portrait of tangent in the record of partaking with two points. Here that turned out for us.

Most important, what we are taught by this picture, so it to those places, where it is needed to search sines and cosines. In the system of denotations accepted by mathematicians, sines always are situated on a vertical line - it upwards-downward. Cosines always are situated on a horizontal - it to the left-right (or aside). That is a complete set will look from 6 trigonometric functions in our variant of denotations. For evidentness a sine and cosine are depicted by a different color and we will add fractional hyphens wherein without them not to do.


Do not be frightened such amount of pictures. That it is represented in overhead part, above a red line, we almost learned already. We will repeat:
a sine - it upwards
a cosine - is aside
a tangent - it to divide a sine into a cosine
Do you see? The half of trigonometric functions we learned already. With the second half, that under a red line, yet simpler - invert that you learned already heels over head. Remaining trigonometric functions are shots reverse already known to us. We swap a numerator and denominator - all is ready already for us.
With a cotangent all is simple. A cotangent is this attitude of cosine toward a sine. With gimbleting of tangent no problems arise up - he has both a numerator and denominator. But as to be with a sine and cosine? We do not have denominators of these shots in fact! Do not worry, any number has a denominator that in mathematics, writing is not accepted is unit. In a secant and cosecant exactly this unit appears in a numerator, and a cosine and sine are written in a denominator.
It is important to memorize! In the pairs of the names of trigonometric functions a secant is a cosine and cosecant - a sine can be only one prefix to on two names. If we take a sine for basis, then a reverse shot will be named cosecant. If we take a cosine, then a reverse shot is named secant, because one prefix to we already used up on a cosine.
It is important to memorize! In the pairs of the names of trigonometric functions a secant - is a cosine and cosecant - a sine can be only one prefix co on two names. If we take a sine for basis, then a reverse shot will be named cosecant. If we take a cosine, then a reverse shot is named secant, because one prefix co we already used up on a cosine.
In principle, it fully sufficiently, in determinations of trigonometric functions to feel, close as an oyster in water. A question remains not found out, that at a sine and cosine to write in a denominator instead of unit. In fact we said in beginning, that trigonometric functions are a result of division(relation) or shot. Do not worry, mathematicians will prompt us, that exactly they want there to see. For this purpose there are determinations of trigonometric functions. We will talk next time about them.
Why is a zero not a number?
Why is a zero not a number? Let us conduct a scientific experiment. We will take any number and will execute the simplest mathematical action - addition or deduction.
Simply so to execute a mathematical action will not turn out. One number and one sign of mathematical action are simply two mathematical symbols, standing alongside. Single character designates a number, the second symbol designates an action.
7 +
7 –
In order that an action happened, it is needed yet something. Only then we will get a result. And this result depends on that we take exactly. If we will take other any number, then the first number will change. The result of this change we write down after equal sign.
7 + 2 = 9
7 – 2 = 5
number + number = result
number - number = result
And that will be, if we will take a not number? For example, will we add salt, will add a paint, will decrease a temperature? That will be with a number, if to salt him? Nothing. A number will remain unchanging.
7 + salt = 7
Now we will try to paint a number.
7 + paint = 7
A number did not change again. But as regarding that, to push in our number in a refrigerator and lower his temperature?
7 - temperature = 7
Why does take place so? Because salt, paint, temperature numbers it is not been. A number and not number inter se do not co-operate. If to take them and make an effort with them to do anything, for us nothing will turn out. What number we took at the beginning, the same we get in the end.
number + not number = number and not number
number - not number = number and not number
Mathematicians and philosophers will argue that a number is an abstract concept that does not exist in the wild, and salt, paint, temperature, is the real things. Exactly from a difference abstract and real nothing takes place. The abstract can not influence on the real, real can not influence on abstract. What, I fully agree with the conclusions of mathematicians and philosophers. They are absolutely right - for a change real the real is needed, for a change abstract the abstract is needed.
In the second part of our experiment we will try to the abstract number to add anything abstract. Well, for example, soul. In hands this thing nobody held, she is not fixed scientific devices. The soul is this cleanly abstract concept. We will look at a result.
7 + the soul = 7
7 - the soul = 7
As see, even many abstract concepts are not able to run the number, because not all abstract concepts are numbers.
Here time to conduct an experiment with a zero, the same abstract concept, as well as number came now. We will add and will take away a zero from a number and will look at a result.
7 + 0 = 7
7 – 0 = 7
As a result of addition or deduction of zero a number remains unchanging. And takes place so because zero, as well as all other not numbers, a number is not. A zero does not possess all those properties that is possessed by numbers.
For plenitude of the conducted experiment it is needed to consider the mathematical operations of increase and division. Multiplying and dividing by a zero in mathematics has a result different from the originally taken number. But let us remember history of development of mathematics.
Addition and deduction appeared at first, an increase and division appeared then. Probably, somewhere a zero appeared after it. There was it in those times, when a faith in God was basis of existence of man. About no results of experiments there could not be speech, if these results conflicted with a faith. Here on this faith and the results of increase and dividing are founded by a zero. Someone said that a zero was a number and in it believed. Someone offered the result of multiplying by a zero - believed in a result. In him we are pin faiths until now: any number increased on a zero equals a zero.
With dividing by a zero there were problems. Nobody was able to offer nothing clever, such, that all believed in it. Mathematical experiments with the results of dividing by a zero give contradictory results and trench upon bases of mathematics. A compromise variant was therefore found is a phrase, "dividing by a zero is impossible". It did not mix to believe that a zero is a number, and did not result in the necessity of revision of other substantive provisions of mathematics. Absence of result of division of number on a zero confirms circumstance that in this case we deal with a not number.
Conclusion: ZERO IS NOT NUMBER
More interesting things on the page "New Math".
Simply so to execute a mathematical action will not turn out. One number and one sign of mathematical action are simply two mathematical symbols, standing alongside. Single character designates a number, the second symbol designates an action.
7 +
7 –
In order that an action happened, it is needed yet something. Only then we will get a result. And this result depends on that we take exactly. If we will take other any number, then the first number will change. The result of this change we write down after equal sign.
7 + 2 = 9
7 – 2 = 5
number + number = result
number - number = result
And that will be, if we will take a not number? For example, will we add salt, will add a paint, will decrease a temperature? That will be with a number, if to salt him? Nothing. A number will remain unchanging.
7 + salt = 7
Now we will try to paint a number.
7 + paint = 7
A number did not change again. But as regarding that, to push in our number in a refrigerator and lower his temperature?
7 - temperature = 7
Why does take place so? Because salt, paint, temperature numbers it is not been. A number and not number inter se do not co-operate. If to take them and make an effort with them to do anything, for us nothing will turn out. What number we took at the beginning, the same we get in the end.
number + not number = number and not number
number - not number = number and not number
Mathematicians and philosophers will argue that a number is an abstract concept that does not exist in the wild, and salt, paint, temperature, is the real things. Exactly from a difference abstract and real nothing takes place. The abstract can not influence on the real, real can not influence on abstract. What, I fully agree with the conclusions of mathematicians and philosophers. They are absolutely right - for a change real the real is needed, for a change abstract the abstract is needed.
In the second part of our experiment we will try to the abstract number to add anything abstract. Well, for example, soul. In hands this thing nobody held, she is not fixed scientific devices. The soul is this cleanly abstract concept. We will look at a result.
7 + the soul = 7
7 - the soul = 7
As see, even many abstract concepts are not able to run the number, because not all abstract concepts are numbers.
Here time to conduct an experiment with a zero, the same abstract concept, as well as number came now. We will add and will take away a zero from a number and will look at a result.
7 + 0 = 7
7 – 0 = 7
As a result of addition or deduction of zero a number remains unchanging. And takes place so because zero, as well as all other not numbers, a number is not. A zero does not possess all those properties that is possessed by numbers.
For plenitude of the conducted experiment it is needed to consider the mathematical operations of increase and division. Multiplying and dividing by a zero in mathematics has a result different from the originally taken number. But let us remember history of development of mathematics.
Addition and deduction appeared at first, an increase and division appeared then. Probably, somewhere a zero appeared after it. There was it in those times, when a faith in God was basis of existence of man. About no results of experiments there could not be speech, if these results conflicted with a faith. Here on this faith and the results of increase and dividing are founded by a zero. Someone said that a zero was a number and in it believed. Someone offered the result of multiplying by a zero - believed in a result. In him we are pin faiths until now: any number increased on a zero equals a zero.
With dividing by a zero there were problems. Nobody was able to offer nothing clever, such, that all believed in it. Mathematical experiments with the results of dividing by a zero give contradictory results and trench upon bases of mathematics. A compromise variant was therefore found is a phrase, "dividing by a zero is impossible". It did not mix to believe that a zero is a number, and did not result in the necessity of revision of other substantive provisions of mathematics. Absence of result of division of number on a zero confirms circumstance that in this case we deal with a not number.
Conclusion: ZERO IS NOT NUMBER
More interesting things on the page "New Math".
Tuesday, February 28, 2012
Modulus of sine
Me it was asked to show method to simplify trigonometric expression, containing the sum of sine and modulus of sine of corner, knowing that corner alpha is finished in 4 fourths. This expression looks so:
|sinA|+sinA
At once I will say honestly, that I a concept do not have, as such expressions are simplified. But about the module of sine I can tell and that will turn out in the total, then. All of you know well, that a sine, as well as all trigonometric functions, can take on positive and negative values. So, sine in the Chinese sticks, that in mathematics read as a "module of sine of corner A", can not have negative values, only positive. When mathematicians are fastidious to touch to the negative numbers, they apply these chopsticks (or modulus of number), as condom at sex, that to be not infected by minus. They rescue the life these, as all numbers in the module from negative grow into positive.

Well now a bit about sign life of sine of corner of А. Sine - it for us upwards and downward on an axis Y-mill from unit to minus units. When corner A from 0 to 180 degrees take on values, all sines of these corners are positive. In this case the chopsticks of the module are the superfluous measure of caution and they can be cast aside. In this range of values of corner A our expression will assume an air:
|sinA|+sinA = sinA+sinA = 2sinA (0 < A < 180)
If value of corner A to increase farther, from 180 to 360 degrees, values of sines of these corners will be negative, id est with a sign " minus". In this case the module begins to play the rock role the fate of our mathematical expression. The value of sine with the module remains positive, and the value of sine without the module becomes negative, as well as it is fixed to all decent sines. What will we get, if from a number we will take away a such is exact number? Correctly, zero. Our expression dies out, as dinosaurs. By the way, if all people always will use condoms during sex, humanity here will die out fully. Effect of the modulus. We will look, that takes place with our expression in this case:
|sinA|+sinA = sinA-sinA = 0 (180 < A < 360)
Application of formulas of bringing trigonometric functions over will give an exactly such result. Thus the module compels us to cast aside in garbage all signs minus, got as a result of transformations.
At corners 0, 180, 360 et cetera degrees our expression will equal a zero, as a zero the values of sine of these corners are equal to.
As all of it it is correct to write down in complete accordance with the rules of mathematical bureaucracy, I do not know. But sense of what be going on, I hope, clear you and you without effort will design this expression in the best kind.
|sinA|+sinA
At once I will say honestly, that I a concept do not have, as such expressions are simplified. But about the module of sine I can tell and that will turn out in the total, then. All of you know well, that a sine, as well as all trigonometric functions, can take on positive and negative values. So, sine in the Chinese sticks, that in mathematics read as a "module of sine of corner A", can not have negative values, only positive. When mathematicians are fastidious to touch to the negative numbers, they apply these chopsticks (or modulus of number), as condom at sex, that to be not infected by minus. They rescue the life these, as all numbers in the module from negative grow into positive.

Well now a bit about sign life of sine of corner of А. Sine - it for us upwards and downward on an axis Y-mill from unit to minus units. When corner A from 0 to 180 degrees take on values, all sines of these corners are positive. In this case the chopsticks of the module are the superfluous measure of caution and they can be cast aside. In this range of values of corner A our expression will assume an air:
|sinA|+sinA = sinA+sinA = 2sinA (0 < A < 180)
If value of corner A to increase farther, from 180 to 360 degrees, values of sines of these corners will be negative, id est with a sign " minus". In this case the module begins to play the rock role the fate of our mathematical expression. The value of sine with the module remains positive, and the value of sine without the module becomes negative, as well as it is fixed to all decent sines. What will we get, if from a number we will take away a such is exact number? Correctly, zero. Our expression dies out, as dinosaurs. By the way, if all people always will use condoms during sex, humanity here will die out fully. Effect of the modulus. We will look, that takes place with our expression in this case:
|sinA|+sinA = sinA-sinA = 0 (180 < A < 360)
Application of formulas of bringing trigonometric functions over will give an exactly such result. Thus the module compels us to cast aside in garbage all signs minus, got as a result of transformations.
At corners 0, 180, 360 et cetera degrees our expression will equal a zero, as a zero the values of sine of these corners are equal to.
As all of it it is correct to write down in complete accordance with the rules of mathematical bureaucracy, I do not know. But sense of what be going on, I hope, clear you and you without effort will design this expression in the best kind.
Tuesday, February 14, 2012
Trigonometric table in radians
This trigonometric table is made for the values of corners in radians. Radians are here given as decimal fractions within two signs after a comma. Value of sine, cosine and tangent given within four signs after a comma. It is such small trigonometric table in radians. You can see the picture Degree-Radian Conversion at the end of the page.
Table of trigonometric values in degrees:




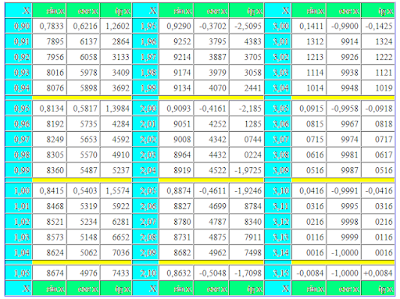
In this trigonometric table the value of corner in radians closes on a 3,15 radian, that corresponds hardly anymore 180 degrees in the degree measure of corners. Here you will not find the value of tangent, equal to unit, value of sine, equal to unit and value of cosine, equal to the zero. In the radian measure of corners to get these values unassisted number of Pi it is impossible. And as a self number of Pi is an endless shot not having the exact meaning, expediency of goniometry in radians is very doubtful. Radians - it, put it mildly, strange unit of measurement.
Values of corner in radians are in blue columns mark the letter of "X". In three columns the values of sin x are given on the right, cos x and tg x for corners in radians. Value of cotangent, secant and cosecant to the table not driven, as these trigonometric functions are reverse shots to driven to the table. For the receipt of values of ctg x, sec x and cosec x in radians, it is needed to divide unit into a tangent, cosine or sine of corresponding corner in radians.
Table of trigonometric values in degrees:
sin cos
tan cot







In this trigonometric table the value of corner in radians closes on a 3,15 radian, that corresponds hardly anymore 180 degrees in the degree measure of corners. Here you will not find the value of tangent, equal to unit, value of sine, equal to unit and value of cosine, equal to the zero. In the radian measure of corners to get these values unassisted number of Pi it is impossible. And as a self number of Pi is an endless shot not having the exact meaning, expediency of goniometry in radians is very doubtful. Radians - it, put it mildly, strange unit of measurement.
Values of corner in radians are in blue columns mark the letter of "X". In three columns the values of sin x are given on the right, cos x and tg x for corners in radians. Value of cotangent, secant and cosecant to the table not driven, as these trigonometric functions are reverse shots to driven to the table. For the receipt of values of ctg x, sec x and cosec x in radians, it is needed to divide unit into a tangent, cosine or sine of corresponding corner in radians.
 |
| Degree-Radian Conversion |
Saturday, February 04, 2012
Trigonometric table tangent cotangent in degrees
Trigonometric table tangent cotangent in degrees - it is the four-valued table of tangents and cotangents in degrees within one minute. A few examples are made at the beginning, as to use this table. For comfort in a table additional navigation elements are plugged with pointing by the name of the names of functions and values of minutes column-wise for every function. Value of degrees and minutes for every trigonometric function distinguished by different colors: for tangents - green, for cotangents - blue. Connotations for minutes are distinguished by yellow.
A trigonometric table for tangents and cotangents consists of two parts. The first part includes tangents from 0 to 75 degrees and cotangents from 15 to 90 degrees. Before to use this table, it is recommended on present examples to find the values of tangents and cotangents on a table and compare results. If all turned out correctly for you, means you can consider itself an experience user of table.





At the use it is necessary to remember this table, that additional values one, two and three minutes for a tangent have a sign plus and at addition added and at deduction subtracted, for a cotangent they have a sign minus and at addition subtracted, and at deduction added. For verification compare the got result to the values of the same name trigonometric functions in the alongside located cells.
The second part of trigonometric table includes tangents from 75 to 90 degrees and cotangents from 0 to 15 degrees. To use this table some simpler, than by the first part.




For a tangent 90 degrees and cotangent 0 degrees a value is not certain. It is so accepted to consider because task on dividing by a zero mathematicians until now so not succeeded to decide.
If you need a trigonometric table of sines and cosines, then she can be found on a separate page.
A trigonometric table for tangents and cotangents consists of two parts. The first part includes tangents from 0 to 75 degrees and cotangents from 15 to 90 degrees. Before to use this table, it is recommended on present examples to find the values of tangents and cotangents on a table and compare results. If all turned out correctly for you, means you can consider itself an experience user of table.






At the use it is necessary to remember this table, that additional values one, two and three minutes for a tangent have a sign plus and at addition added and at deduction subtracted, for a cotangent they have a sign minus and at addition subtracted, and at deduction added. For verification compare the got result to the values of the same name trigonometric functions in the alongside located cells.
The second part of trigonometric table includes tangents from 75 to 90 degrees and cotangents from 0 to 15 degrees. To use this table some simpler, than by the first part.





For a tangent 90 degrees and cotangent 0 degrees a value is not certain. It is so accepted to consider because task on dividing by a zero mathematicians until now so not succeeded to decide.
If you need a trigonometric table of sines and cosines, then she can be found on a separate page.
Tuesday, January 10, 2012
Trigonometric table of sines and cosines
The trigonometric table of values of sines and cosines within one minute is counted on blondes. For comfort of the use for sines and cosines distinguished this table of value of corners by different colors. For sines the blue color of cells is accepted with degrees and by minutes. For cosines the green background of cells is accepted. A yellow background is distinguish the values of minutes that if necessary is added or subtracted from tabular values.


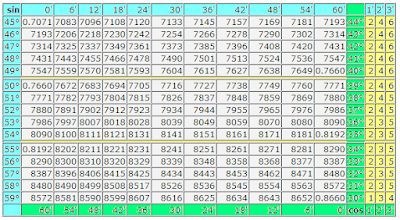
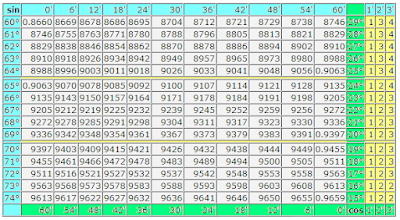

Usually it is not accepted so in detail to give a navigation on a trigonometric table. Firstly, a table is counted on experience users by mathematics. Secondly, publishers from old times produce these tables in a blackly white variant and in every way save printer's ink on a navigation on a trigonometric table.
I hope, such registration will not give to lose way you even in the middle of this table and you will not entangle sines with cosines at the search of their values. By the way, the trigonometric table of sines and cosines presents the values of these trigonometric functions for corners from 0 to 90 degrees. For other values of corners can use a trigonometric circle as a crib.
If you need more exact calculation of values of trigonometric functions, then can take advantage of calculator. How to use the table of Брадиса, we will understand next time. Specially for those, whoever knows.






Usually it is not accepted so in detail to give a navigation on a trigonometric table. Firstly, a table is counted on experience users by mathematics. Secondly, publishers from old times produce these tables in a blackly white variant and in every way save printer's ink on a navigation on a trigonometric table.
I hope, such registration will not give to lose way you even in the middle of this table and you will not entangle sines with cosines at the search of their values. By the way, the trigonometric table of sines and cosines presents the values of these trigonometric functions for corners from 0 to 90 degrees. For other values of corners can use a trigonometric circle as a crib.
If you need more exact calculation of values of trigonometric functions, then can take advantage of calculator. How to use the table of Брадиса, we will understand next time. Specially for those, whoever knows.
Subscribe to:
Posts (Atom)