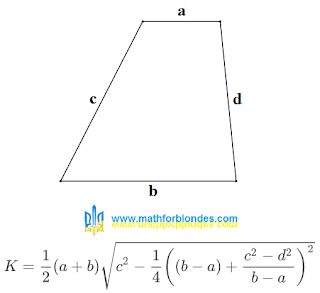
|
| Infinite set |
Alpha denotes a real number. The equal sign in the above expressions indicates that if you add a number or infinity to infinity, nothing will change, the result will be the same infinity. If we take an infinite number of natural numbers as an example, then the considered examples can be represented in the following form:
 |
| The set of natural numbers |
To illustrate their point, mathematicians have come up with . Personally, I look at all these methods, as the dances of shamans with tambourines. In fact, they all boil down to the fact that either part of the rooms are not occupied and new guests are accommodated in them, or that some of the visitors are thrown out into the corridor to make room for guests (very humanly). I outlined my view on such decisions here in the form of a fantastic story about the Blonde. What is my reasoning based on? Relocating an infinite number of visitors requires an infinitely long time. After we vacated the first room for the guest, one of the visitors will always walk along the corridor from his room to the next one until the end of the century. Of course, the time factor can be stupidly ignored. It is mathematicians who are trying to manipulate hotel room numbers, convincing us that you can insert something that, in principle, cannot be inserted.
I will demonstrate the logic of my reasoning to you as an example of an infinite number of natural numbers. First you need to answer a very simple question: how many sets of natural numbers exist - one or many? The correct answer to this question does not exist, since we thought up the numbers ourselves; in Nature there are no numbers. Yes, Nature knows how to count, but for this she uses other mathematical tools that are not familiar to us. As Nature believes, I will tell you another time. Since we came up with numbers, we will decide how many sets of natural numbers exist. Consider both options, as befits a real scientist.
Option one. "Let us be given" one single set of natural numbers, which lies serenely on the shelf. We take this set from the shelf. Everything, there are no other natural numbers on the shelf and there is nowhere to take them. We cannot add one to this set, since we already have one. And if you really want to? No problem. We can take a unit from the set already taken by us and return it to the shelf. After that, we can take a unit from the shelf and add it to what we have left. As a result, we again get an infinite number of natural numbers. All our manipulations can be written like this:
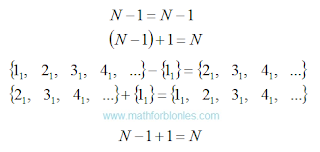 |
| One set of natural numbers |
I wrote down the actions in the algebraic notation and in the notation adopted in set theory, with a detailed listing of the elements of the set. The subscript indicates that the set of positive integers is one and only. It turns out that the set of natural numbers will remain unchanged only if you subtract unit from it and add the same unit.
Option two. We have on the shelf many different infinite sets of natural numbers. I emphasize - DIFFERENT, despite the fact that they are practically indistinguishable. We take one of these sets. Then we take unit from another set of natural numbers and add to the set we have already taken. We can even add up two sets of natural numbers. Here's what we get:
 |
| Many sets of natural numbers |
The subscripts “one” and “two” indicate that these elements belonged to different sets. Yes, if you add one to an infinite set, the result will also be an infinite set, but it will not be the same as the original set. If we add another infinite set to one infinite set, the result is a new infinite set consisting of elements of the first two sets.
Set of natural numbers are used for counting in the same way as a ruler for measurements. Now imagine that you added one centimeter to a ruler. This will be a different a ruler, not equal to the original.
You can accept or not accept my reasoning - this is your personal matter. But if you ever run into mathematical problems, think about whether you are following the path of false reasoning, trodden by generations of mathematicians. After all, classes in mathematics, first of all, form a stable stereotype of thinking in us, and only then they add mental abilities to us (or vice versa, deprive us of free thinking).