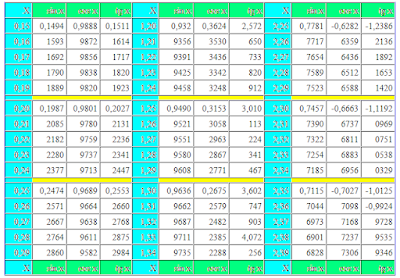
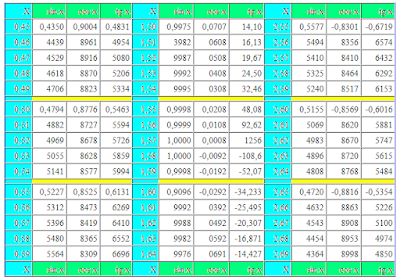
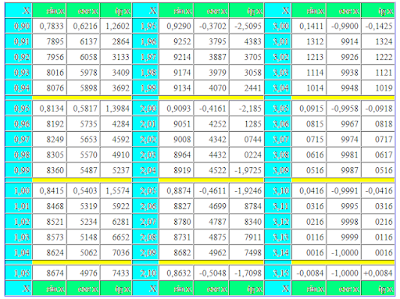
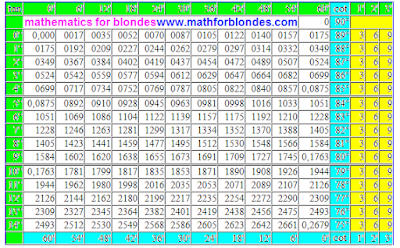
|sinA|+sinA
At once I will say honestly, that I a concept do not have, as such expressions are simplified. But about the module of sine I can tell and that will turn out in the total, then. All of you know well, that a sine, as well as all trigonometric functions, can take on positive and negative values. So, sine in the Chinese sticks, that in mathematics read as a "module of sine of corner A", can not have negative values, only positive. When mathematicians are fastidious to touch to the negative numbers, they apply these chopsticks (or modulus of number), as condom at sex, that to be not infected by minus. They rescue the life these, as all numbers in the module from negative grow into positive.

Well now a bit about sign life of sine of corner of А. Sine - it for us upwards and downward on an axis Y-mill from unit to minus units. When corner A from 0 to 180 degrees take on values, all sines of these corners are positive. In this case the chopsticks of the module are the superfluous measure of caution and they can be cast aside. In this range of values of corner A our expression will assume an air:
|sinA|+sinA = sinA+sinA = 2sinA (0 < A < 180)
If value of corner A to increase farther, from 180 to 360 degrees, values of sines of these corners will be negative, id est with a sign " minus". In this case the module begins to play the rock role the fate of our mathematical expression. The value of sine with the module remains positive, and the value of sine without the module becomes negative, as well as it is fixed to all decent sines. What will we get, if from a number we will take away a such is exact number? Correctly, zero. Our expression dies out, as dinosaurs. By the way, if all people always will use condoms during sex, humanity here will die out fully. Effect of the modulus. We will look, that takes place with our expression in this case:
|sinA|+sinA = sinA-sinA = 0 (180 < A < 360)
Application of formulas of bringing trigonometric functions over will give an exactly such result. Thus the module compels us to cast aside in garbage all signs minus, got as a result of transformations.
At corners 0, 180, 360 et cetera degrees our expression will equal a zero, as a zero the values of sine of these corners are equal to.
As all of it it is correct to write down in complete accordance with the rules of mathematical bureaucracy, I do not know. But sense of what be going on, I hope, clear you and you without effort will design this expression in the best kind.