Monday, August 23, 2010
How is a devidend named, that under a line?
In a fraction under a line a divizor is written. He is named denominator. If you must find the denominator of fraction, it is needed to search him under a fractional line. Type, how under a bed to glance. All denominators are always hidden under a fractional line, as under a bed. As a denominator there can be both numbers and whole mathematical expressions, sometimes very large.
Enter numbers the difference of numbers zero and twenty
"Enter numbers the difference of numbers 0 (zero) and 20 (twenty)" - a similar task very often meets in the Internet. Interesting that I do not know exactly, how her it is correct to decide. Omniscient Wikipedia reports bashfully, that a difference of numbers is a result of deduction of two numbers. But here, as correct to execute the action of deduction, this collection of wisdom holds back. In fact two variants of decision of this task are possible:
1. From the first number to subtract second 0 - 20 = - 20 (to take away zero twenty evened minus twenty)
2. From a greater number to subtract less 20 - 0 = 20 (twenty to take away zero evened twenty)
As see, we got two different answers. In one there is a sign minus, in other the sign minus it is not. Now we will begin to ratiocinate. A similar task is set by the program, the programs are written by programmers. I doubt that they remember about such nuances of school mathematics, as a sign is minus in the results of deduction of numbers. Therefore I suggest to operate by the tested method - by a scientific method. We will enter in a window numbers 20 (twenty) without a sign minus.
If Sim-Sim accepted our answer and opened access to treasures of the Internet, our experiment is completed. If a window answered us, that we are not right, then this iron will give out other pair of numbers to us.
Now we already the experienced users of this window. If it is again written us, for example, "Enter numbers the difference of numbers 0 (zero) and 16 (sixteen)", then we already know exactly, that it is needed in a window to enter - 16 (minus sixteen), with a mark minus ahead.
(zero minus sixteen evened minus sixteen)
If a window will write something type "Enter numbers the difference of numbers 1 (one) and 0 (zero)", then we without every vibrations enter a number 1 (one). In fact in this case and from the first number to take away second, and from a greater number to take away less, give an identical result is a positive number, without every signs minus.
(one minus zero evened one)
For all pair of numbers, if the first number anymore than second, a result will always be positive. For example:
(twenty minus fourteen evened six)
In a window it is needed to enter a number 6 (six, it a number is such).
In case if the program will take in head to flash the erudition and will give out to you a task "Enter numbers the difference of numbers 0 (zero) and 0 (zero)", not frightened and bravely enter a number 0 (zero)!
(zero minus zero evened zero)
Lighthouses for blondes. All, who searches answers for a question "That means enter the difference of numbers?" - you need to pass to this page!
1. From the first number to subtract second 0 - 20 = - 20 (to take away zero twenty evened minus twenty)
2. From a greater number to subtract less 20 - 0 = 20 (twenty to take away zero evened twenty)
As see, we got two different answers. In one there is a sign minus, in other the sign minus it is not. Now we will begin to ratiocinate. A similar task is set by the program, the programs are written by programmers. I doubt that they remember about such nuances of school mathematics, as a sign is minus in the results of deduction of numbers. Therefore I suggest to operate by the tested method - by a scientific method. We will enter in a window numbers 20 (twenty) without a sign minus.
If Sim-Sim accepted our answer and opened access to treasures of the Internet, our experiment is completed. If a window answered us, that we are not right, then this iron will give out other pair of numbers to us.
Now we already the experienced users of this window. If it is again written us, for example, "Enter numbers the difference of numbers 0 (zero) and 16 (sixteen)", then we already know exactly, that it is needed in a window to enter - 16 (minus sixteen), with a mark minus ahead.
0 - 16 = -16
(zero minus sixteen evened minus sixteen)
If a window will write something type "Enter numbers the difference of numbers 1 (one) and 0 (zero)", then we without every vibrations enter a number 1 (one). In fact in this case and from the first number to take away second, and from a greater number to take away less, give an identical result is a positive number, without every signs minus.
1 - 0 = 1
(one minus zero evened one)
For all pair of numbers, if the first number anymore than second, a result will always be positive. For example:
20 - 14 = 6
(twenty minus fourteen evened six)
In a window it is needed to enter a number 6 (six, it a number is such).
In case if the program will take in head to flash the erudition and will give out to you a task "Enter numbers the difference of numbers 0 (zero) and 0 (zero)", not frightened and bravely enter a number 0 (zero)!
0 - 0 = 0
(zero minus zero evened zero)
Lighthouses for blondes. All, who searches answers for a question "That means enter the difference of numbers?" - you need to pass to this page!
Devidend of fraction as named?
The devidend of fraction is named numerator. A numerator is always written above a fractional line. It is needed nowhere to peep in search of numerator of fraction, type under a bed. A numerator of fraction is always on the most prominent position, from above fractional line, as a prince on a pea. As a numerator there can be numbers or mathematical expressions.
Sunday, August 22, 2010
Greatest natural number
The greatest natural number is not present and can not be. Mathematicians at that rate it is said that the natural series of numbers are infinite. It is written so even in Wikipedia.
Let us understand, why takes place so. We will assume, we thought of the greatest natural number. For simplicity we will take the natural number of "Googol" is unit with one hundred zeros, ten in a hundredth degree.
Yes, yes, not surprised, the steepest searching machine of the Internet Google is named after the number of Googol! It and not surprisingly, in fact created a searching machine in distant, distant 1998 to the year two students Larry Page and Sergey Brin. You present, 12 (twelve!) years back there was not Google! How did people the Internet use?! But we were a bit distracted...
And so, we consider that the greatest natural number is a number of Googol. That us does interfere with to finish writing to this greatest number another, one hundred first, zero? We take a pen in hands, we look around on parties, that nobody saw, and we finish writing zero. Our greatest natural number increased tenfold and became yet more! Wow! We finish writing yet zero, and then yet, and yet... Through time, writing zeros already nowhere, and they (zeros) all do not end in any way. We reach the next piece of wallpapers, prepared for repair of antechamber, and we keep writing. On the middle of roll paste is closed, and the greatest natural number we so not wrote. If to buy up all ball-point pens in a booth and all wallpapers in a building shop, it how many zeros is it possible to finish writing? Will this be the greatest natural number? No, building магизинов with wallpapers very much, it is possible yet to write and write... Amusing, certainly, to spend right through life and all dad money on scribble of one number, but there are entertainments much more interesting.
Let now we will look at the problem of the greatest natural number on the other hand. If a child is able to consider only to five, then for such child pentad will be the greatest in the world number. But we know that well, that is yet very much many numbers which more pentad. Simply we know mathematics much better than child. In course of time a child will laugh at the "greatest in the world number".
There are no grounds to disbelieve mathematicians, to asserting, that the series of natural numbers are infinite and the greatest natural number can not be.
I tried to find the construction of the greatest number, but omniscient Wikipedia is quiet even on that score, and a search on the Internet is given out by different garbage. Therefore I present the own variant of the GREATEST NUMBER IN THE WORLD. It will look as endlessness in a degree endlessness, in a degree endlessness, in a degree endlessness... and so for ever and ever. Instead of mark of endlessness can put any natural number, except unit. What a greater number you will put, the steeper there will be flight to unattainable.
Here it and there is the GREATEST NUMBER IN MATHEMATICS, more precisely, his mathematical construction. If someone knows from erudites, how this is named, write in comments, with pleasure I will correct the name. Not forget to give reference to the information generator. Similar principle of search of the greatest number is much more effective than dull finishing writing of zeros.
By the way, little numbers at which small zeros grew quite have the famous enough names own. Glance on a page "Unit and twenty one zero", if want to become acquainted with them closer. Every blonde is under an obligation to know, what a millionaire differs from a multimillionaire. Otherwise as will you choose to itself a husband?
Let us understand, why takes place so. We will assume, we thought of the greatest natural number. For simplicity we will take the natural number of "Googol" is unit with one hundred zeros, ten in a hundredth degree.
Yes, yes, not surprised, the steepest searching machine of the Internet Google is named after the number of Googol! It and not surprisingly, in fact created a searching machine in distant, distant 1998 to the year two students Larry Page and Sergey Brin. You present, 12 (twelve!) years back there was not Google! How did people the Internet use?! But we were a bit distracted...
And so, we consider that the greatest natural number is a number of Googol. That us does interfere with to finish writing to this greatest number another, one hundred first, zero? We take a pen in hands, we look around on parties, that nobody saw, and we finish writing zero. Our greatest natural number increased tenfold and became yet more! Wow! We finish writing yet zero, and then yet, and yet... Through time, writing zeros already nowhere, and they (zeros) all do not end in any way. We reach the next piece of wallpapers, prepared for repair of antechamber, and we keep writing. On the middle of roll paste is closed, and the greatest natural number we so not wrote. If to buy up all ball-point pens in a booth and all wallpapers in a building shop, it how many zeros is it possible to finish writing? Will this be the greatest natural number? No, building магизинов with wallpapers very much, it is possible yet to write and write... Amusing, certainly, to spend right through life and all dad money on scribble of one number, but there are entertainments much more interesting.
Let now we will look at the problem of the greatest natural number on the other hand. If a child is able to consider only to five, then for such child pentad will be the greatest in the world number. But we know that well, that is yet very much many numbers which more pentad. Simply we know mathematics much better than child. In course of time a child will laugh at the "greatest in the world number".
There are no grounds to disbelieve mathematicians, to asserting, that the series of natural numbers are infinite and the greatest natural number can not be.
I tried to find the construction of the greatest number, but omniscient Wikipedia is quiet even on that score, and a search on the Internet is given out by different garbage. Therefore I present the own variant of the GREATEST NUMBER IN THE WORLD. It will look as endlessness in a degree endlessness, in a degree endlessness, in a degree endlessness... and so for ever and ever. Instead of mark of endlessness can put any natural number, except unit. What a greater number you will put, the steeper there will be flight to unattainable.
∞∞∞∞···∞···
Here it and there is the GREATEST NUMBER IN MATHEMATICS, more precisely, his mathematical construction. If someone knows from erudites, how this is named, write in comments, with pleasure I will correct the name. Not forget to give reference to the information generator. Similar principle of search of the greatest number is much more effective than dull finishing writing of zeros.
By the way, little numbers at which small zeros grew quite have the famous enough names own. Glance on a page "Unit and twenty one zero", if want to become acquainted with them closer. Every blonde is under an obligation to know, what a millionaire differs from a multimillionaire. Otherwise as will you choose to itself a husband?
Saturday, August 21, 2010
What number are the natural series of numbers begun with?
The natural series of numbers are begun with a number 0 (zero). Number 0 (zero) is the least natural number.
For the Russian blondes it was farther written following. In translating into the language of blondes: the littlest natural number - it 1 (one, unit). The littlest natural number has really two names. Probably, one from a dad, second from a mother))) I will remind that in Russian mathematics zero is not a natural number!
For the Russian blondes it was farther written following. In translating into the language of blondes: the littlest natural number - it 1 (one, unit). The littlest natural number has really two names. Probably, one from a dad, second from a mother))) I will remind that in Russian mathematics zero is not a natural number!
Friday, August 20, 2010
What natural numbers smaller five?
Among natural numbers there are five numbers which smaller 5 (five). It is numbers 0 (zero), 1 (one), 2 (two), 3 (three) and 4 (four). We will repeat for evidentness in large. Natural numbers smaller five:
Checking up the rightness of my reasoning is possible, overseeing in the table of natural numbers.
0; 1; 2; 3; 4
Checking up the rightness of my reasoning is possible, overseeing in the table of natural numbers.
Thursday, August 19, 2010
Legend about Sine and Cosine
I
n ancient, ancient times, when the world was quite another, and quite another laws governed in him, two nice tiny creatures, Sine and Cosine, went to school. They lived in long and friendly family of Numbers. Beat Sine and Cosine bytwins - nobody could distinguish them, even Lord of All Mathematician. Many different amusing histories happened with twins from their alikeness. They especially loved to jolly above Gods which built the worlds and often asked for a help at Numbers. Though quite tiny were Sine and Cosine as compared to other Numbers, but work was executed very important. One of twins will help to create a next universe God, God thanks Sine - and it, appears, Cosine tried in all...
Long proceeded so, or not, but once at school, sitting after one school desk, very strange phrases read Sine and Cosine. In the textbook of Sine it was written: "Sine is main, and Cosine helps him". In the textbook of Cosine it was written: "Cosine is main, and Sine helps him". In all other the textbooks were absolutely identical. Brothers were thoughtful right here, and then began to argue, who of them main. Each of them asserted that main he, and in his textbook it is written correctly.
Brothers argued long, finally, asked senior Numbers:
"Who of us main?"
Wise Numbers looked at textbooks, looked at brothers said:
"Change inter se textbooks - and all problems will disappear!"
But, neither Sine nor Cosine wanted to become helpers, they wanted to be only main! Everybody grasped the book and with renewed strength a dispute flamed up between them.
Then brothers appealed to Gods. Many reasonable creatures are known by Gods and with all able to get along with. They know how to settle a dispute.
"Who of us main? What book is it correctly written in?" - asked Sine and Cosine Gods. Gods looked on two absolutely identical tiny creations, smiled and said:
"It is not necessary blindly to believe in everything, that it is written in books. There can be a misprint in any book. Throw out these textbooks and live by the mind, it is time you to become adults."
Sine and Cosine got angry, hid the books a little rather from extraneous eyes. They became stealthily from each other to read each the book, more precisely, each the line about itself.
Long would proceed so, but once, on a call one of Gods, both brothers came for help. Instead of that to help God in his work, Sine and Cosine undertook a dispute inter se. God got angry and sent brothers to Mathematics.
To be continued.
 |
| Legend about Sine and Cosine. Вeginning. |
n ancient, ancient times, when the world was quite another, and quite another laws governed in him, two nice tiny creatures, Sine and Cosine, went to school. They lived in long and friendly family of Numbers. Beat Sine and Cosine bytwins - nobody could distinguish them, even Lord of All Mathematician. Many different amusing histories happened with twins from their alikeness. They especially loved to jolly above Gods which built the worlds and often asked for a help at Numbers. Though quite tiny were Sine and Cosine as compared to other Numbers, but work was executed very important. One of twins will help to create a next universe God, God thanks Sine - and it, appears, Cosine tried in all...
Long proceeded so, or not, but once at school, sitting after one school desk, very strange phrases read Sine and Cosine. In the textbook of Sine it was written: "Sine is main, and Cosine helps him". In the textbook of Cosine it was written: "Cosine is main, and Sine helps him". In all other the textbooks were absolutely identical. Brothers were thoughtful right here, and then began to argue, who of them main. Each of them asserted that main he, and in his textbook it is written correctly.
Brothers argued long, finally, asked senior Numbers:
"Who of us main?"
Wise Numbers looked at textbooks, looked at brothers said:
"Change inter se textbooks - and all problems will disappear!"
But, neither Sine nor Cosine wanted to become helpers, they wanted to be only main! Everybody grasped the book and with renewed strength a dispute flamed up between them.
Then brothers appealed to Gods. Many reasonable creatures are known by Gods and with all able to get along with. They know how to settle a dispute.
"Who of us main? What book is it correctly written in?" - asked Sine and Cosine Gods. Gods looked on two absolutely identical tiny creations, smiled and said:
"It is not necessary blindly to believe in everything, that it is written in books. There can be a misprint in any book. Throw out these textbooks and live by the mind, it is time you to become adults."
Sine and Cosine got angry, hid the books a little rather from extraneous eyes. They became stealthily from each other to read each the book, more precisely, each the line about itself.
Long would proceed so, but once, on a call one of Gods, both brothers came for help. Instead of that to help God in his work, Sine and Cosine undertook a dispute inter se. God got angry and sent brothers to Mathematics.
To be continued.
Wednesday, August 18, 2010
Multiplication by zero
Multiplication by zero is possible, rules of mathematics multiplication by zero is not forbidden. Any number, multiplication by zero, will equal zero. If a whole or fractional number multiplication by zero, zero will ensue.
We will consider the example of multiplication by zero of integer. How many will it be, if 2 (two) to multiplication by 0 (zero)?
Decision: if 2 (two) to multiplication by 0 (zero), 0 (zero) will turn out.
Example of multiplication by zero of broken number. How many will it be, if 0,25 (zero whole twenty five hundredth) to multiplication by 0 (zero)?
Decision: if 0,25 (zero whole twenty five hundredth) to multiplication by 0 (zero), 0 (zero) will turn out.
If to multiplication a positive or negative number by zero, zero will turn out. A number zero does not have sign, therefore signs a plus or minus before zero is not put. Examples of multiplication of positive whole and fractional numbers are made a higher.
Example of multiplication by zero of negative number. How many will it be, if -2 (minus two) to multiplication by 0 (zero)?
Decision: if -2 (minus two) to multiplication by zero, there will be 0 (zero).
We will consider the example of multiplication by zero of integer. How many will it be, if 2 (two) to multiplication by 0 (zero)?
2 х 0 = 0
Decision: if 2 (two) to multiplication by 0 (zero), 0 (zero) will turn out.
Example of multiplication by zero of broken number. How many will it be, if 0,25 (zero whole twenty five hundredth) to multiplication by 0 (zero)?
0,25 х 0 = 0
Decision: if 0,25 (zero whole twenty five hundredth) to multiplication by 0 (zero), 0 (zero) will turn out.
If to multiplication a positive or negative number by zero, zero will turn out. A number zero does not have sign, therefore signs a plus or minus before zero is not put. Examples of multiplication of positive whole and fractional numbers are made a higher.
Example of multiplication by zero of negative number. How many will it be, if -2 (minus two) to multiplication by 0 (zero)?
-2 х 0 = 0
Decision: if -2 (minus two) to multiplication by zero, there will be 0 (zero).
Tuesday, August 17, 2010
Table division by zero
Division by zero is forbidden. Any number, positive or negative, whole or shot, to divide by zero is forbidden. Mathematicians say that the result of division by zero is undefined. Therefore a division table by zero will look so:
If to designate any number through а, then a division table by zero for any numbers will consist only of one line (last line).
Why is the result of division by zero undefined? Because any number multiplied by zero equals zero. Since the mathematical operation of division is the inverse of the mathematical operation of multiplication, division by zero results in all the numbers at once. And mathematicians want to have one specific number.
Is it possible to solve the problem of division by zero? Yes, this problem can be solved. As a result of dividing by zero of a specific number, you will get another specific number. But this requires a much better understanding of mathematics.
I solved this problem. But at the same time, my views on some of the statements of mathematicians have changed dramatically. I spent a lot of time on this. Here you can compare your views on mathematics with the way I see it.
 |
| Table division by zero |
If to designate any number through а, then a division table by zero for any numbers will consist only of one line (last line).
Why is the result of division by zero undefined? Because any number multiplied by zero equals zero. Since the mathematical operation of division is the inverse of the mathematical operation of multiplication, division by zero results in all the numbers at once. And mathematicians want to have one specific number.
Is it possible to solve the problem of division by zero? Yes, this problem can be solved. As a result of dividing by zero of a specific number, you will get another specific number. But this requires a much better understanding of mathematics.
I solved this problem. But at the same time, my views on some of the statements of mathematicians have changed dramatically. I spent a lot of time on this. Here you can compare your views on mathematics with the way I see it.
Monday, August 16, 2010
Division by zero
It is accepted to consider in mathematics, that division by zero not possibly, as a result of division of number by zero can not be certain. Yet mathematicians it is said that division of number by zero behaves to the mathematical operations, to not making sense. Wikipedia asserts on this occasion, that in arithmetic, division by a zero is forbidden. Therefore, when in examples there is division by zero, it is said that an example does not have a decision, as division by zero is forbidden. This mathematical rule behaves to all, even to the blondes.
It becomes firmly established in very clever mathematical books, that division by zero possibly. More precisely, mathematicians thought of sly tricks, what this division by zero to go round a side. They are sure that it succeeded them. So, if in conversation with a clever mathematician, you will hear a phrase "I am able to divide by zero!", not surprised, your interlocutor believes sincerely, that it is possible.
It becomes firmly established in very clever mathematical books, that division by zero possibly. More precisely, mathematicians thought of sly tricks, what this division by zero to go round a side. They are sure that it succeeded them. So, if in conversation with a clever mathematician, you will hear a phrase "I am able to divide by zero!", not surprised, your interlocutor believes sincerely, that it is possible.
Sunday, August 15, 2010
Sine is 30 degrees, sin 30
>Sine 30 degrees are evened by the one second or zero whole five tenth.
In the radian measure sine of corners 30 degrees correspond a sine π/6:
Oddly enough, but justly and reverse equality, which asserts that sine π/6 (sin pi/6) equal a sine 30 degrees:
A sine pi / 6 is evened similarly one second or zero whole five tenth.
It was for blondes. For brunettes and bald academicians of mathematical sciences it is possible to write down all of it in a general view, let untangle:
For complete happiness here obviously the picture of sine 30 degrees is not enough. Surprise! And she:
I hope, the first part of task I decided and I succeeded to explain to the blondes, what the sine of thirty degrees is equal to. It is now needed to decide the second half of task, with which all academy of mathematical sciences, together taken, is unable to manage even. It is needed in the Internet to find blondes which search a sine 30 degrees. Will I try to be armed with logic of blondes and I will transfer below searching queries which blondes can enter in the searching systems at the search of answer for a question: what is a sine equal to 30 degrees? And so, searching queries, dilute my comments, in order the searching systems did not separate my creation from blondes.
Sine - it mathematicians collate the knowledge with the Internet.
Sine, cosine - the authority of mathematicians appeared, to check, as mathematicians collated the knowledge.
A sine of corner - is botanists spectacled, future of Bills Gatesis, comb the clever turnips and try to remember the school course of mathematics.
Sine of degrees - smart schoolboys pelt the question on the way, what quicker cut with this nasty thing and continue a game.
Table of sines, tangents - conscientious schoolboys and respectable brunettes scraped away all cognitions in trigonometry and try to collate them with the Internet.
A value of sine - is mathematicians, after the long wandering on sites with blondes, at last understood how it is better to formulate a searching query.
Values of cosines and sines - mathematicians remembered suddenly, that by a not sine single trigonometry lives by.
Is a sine what equal to? - and the first signs of presence of blondes in the Internet with their appealing spontaneity of intercourse, even with a computer.
Sines and cosines of corners. Table of values of sines. The sine of corner is equal - it mothers try to check up, as their children did lessons.
How to find a sine? - it is already the typical question of the confused blonde.
Sine of acute angle. Sine and cosine 30 - are mothers hardly, but already begin to understand that requires to be found in a task.
A sine of number - is poor mothers, they are even unaware that corners can be measured by radians.
A sine is alpha - mothers remembered, by what letter once at school they designated corners.
Calculator of sines - for help clever dads come helpless mothers.
How to find the sine of corner? - clever dads found the calculator of sine, it is now needed to know, how to use this thing.
Geometry is a sine, cosine. To get the table of sines. Values of sines of corners - it children unstucked from the virtual games and try to prove to the clever dads, that dads not correctly press on the buttons of calculator, because the sine of corner can not equal three jars of beer.
Calculations of sine - mathematicians-theorists try to steal job of mathematicians of the applied sciences performances.
To calculate a sine - it the mathematicians of the applied sciences steal job of the colleagues performances.
Sine of endlessness - it already physicists try to check up the calculations of mathematicians.
Being of sine - blondes try to know, where sines live.
Trigonometric sine - all discovered in surprise, that sines were not only in mathematics.
How many sine 30 - is a zero whole five tenth.
How many sin 30 is equal - so much, zero five.
How many will a sine be 30? - it is a question, certainly, interesting...
A table is sin alpha of 30 degrees - not quite table, but a sine and 30 degrees are exactly.
Numbers from which sines natural are - mathematicians, a blonde put question. Are there variants of answers? Honour of full-dress uniform is put on kitty.
Who can explain why sine 30 degrees 1/2 is equal? - well, infant prodigies, blonde put question. I specifically wrote the page "Why is the sine of 30 degrees equal to 1/2?"
sin 30° = 1/2 or sin 30° = 0,5
In the radian measure sine of corners 30 degrees correspond a sine π/6:
sin 30° = sin π/6
Oddly enough, but justly and reverse equality, which asserts that sine π/6 (sin pi/6) equal a sine 30 degrees:
sin π/6 = sin 30°
A sine pi / 6 is evened similarly one second or zero whole five tenth.
sin π/6 = 1/2 or sin π/6 = 0,5
It was for blondes. For brunettes and bald academicians of mathematical sciences it is possible to write down all of it in a general view, let untangle:
sin 30° = sin π/6 = 1/2 = 0,5
For complete happiness here obviously the picture of sine 30 degrees is not enough. Surprise! And she:
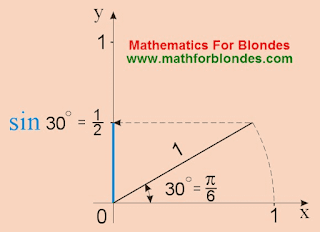 |
| Sine is 30 degrees |
I hope, the first part of task I decided and I succeeded to explain to the blondes, what the sine of thirty degrees is equal to. It is now needed to decide the second half of task, with which all academy of mathematical sciences, together taken, is unable to manage even. It is needed in the Internet to find blondes which search a sine 30 degrees. Will I try to be armed with logic of blondes and I will transfer below searching queries which blondes can enter in the searching systems at the search of answer for a question: what is a sine equal to 30 degrees? And so, searching queries, dilute my comments, in order the searching systems did not separate my creation from blondes.
Sine - it mathematicians collate the knowledge with the Internet.
Sine, cosine - the authority of mathematicians appeared, to check, as mathematicians collated the knowledge.
A sine of corner - is botanists spectacled, future of Bills Gatesis, comb the clever turnips and try to remember the school course of mathematics.
Sine of degrees - smart schoolboys pelt the question on the way, what quicker cut with this nasty thing and continue a game.
Table of sines, tangents - conscientious schoolboys and respectable brunettes scraped away all cognitions in trigonometry and try to collate them with the Internet.
A value of sine - is mathematicians, after the long wandering on sites with blondes, at last understood how it is better to formulate a searching query.
Values of cosines and sines - mathematicians remembered suddenly, that by a not sine single trigonometry lives by.
Is a sine what equal to? - and the first signs of presence of blondes in the Internet with their appealing spontaneity of intercourse, even with a computer.
Sines and cosines of corners. Table of values of sines. The sine of corner is equal - it mothers try to check up, as their children did lessons.
How to find a sine? - it is already the typical question of the confused blonde.
Sine of acute angle. Sine and cosine 30 - are mothers hardly, but already begin to understand that requires to be found in a task.
A sine of number - is poor mothers, they are even unaware that corners can be measured by radians.
A sine is alpha - mothers remembered, by what letter once at school they designated corners.
Calculator of sines - for help clever dads come helpless mothers.
How to find the sine of corner? - clever dads found the calculator of sine, it is now needed to know, how to use this thing.
Geometry is a sine, cosine. To get the table of sines. Values of sines of corners - it children unstucked from the virtual games and try to prove to the clever dads, that dads not correctly press on the buttons of calculator, because the sine of corner can not equal three jars of beer.
Calculations of sine - mathematicians-theorists try to steal job of mathematicians of the applied sciences performances.
To calculate a sine - it the mathematicians of the applied sciences steal job of the colleagues performances.
Sine of endlessness - it already physicists try to check up the calculations of mathematicians.
Being of sine - blondes try to know, where sines live.
Trigonometric sine - all discovered in surprise, that sines were not only in mathematics.
How many sine 30 - is a zero whole five tenth.
How many sin 30 is equal - so much, zero five.
How many will a sine be 30? - it is a question, certainly, interesting...
A table is sin alpha of 30 degrees - not quite table, but a sine and 30 degrees are exactly.
Numbers from which sines natural are - mathematicians, a blonde put question. Are there variants of answers? Honour of full-dress uniform is put on kitty.
Who can explain why sine 30 degrees 1/2 is equal? - well, infant prodigies, blonde put question. I specifically wrote the page "Why is the sine of 30 degrees equal to 1/2?"
Saturday, August 14, 2010
How does a rectangular trapezoid look?
A rectangular trapezoid (also called right-angled trapezoid, right trapezoid) has such kind:
A rectangular trapezoid always has two right angles. On a picture direct corners are marked little squares in tops A and D. Direct corners can be situated in two any contiguous tops of trapezoid.
On this picture of rectangular trapezoid direct corners are located in tops B and С.
In mathematics there is determination of rectangular trapezoid, which over is brought and in Wikipedia: the rectangular is name a trapezoid at which even one corner of line. This classic determination of rectangular trapezoid, bluntly rewritten from sacred mathematical books. In Euclidean geometry a rectangular trapezoid always has two lines of corner, as two sides trapezoids, called grounds, are parallel. Segment BC, formative a direct corner with founding of АВ, will be always perpendicular to the second founding of CD. With one or three direct corners there can be only a curvilinear rectangular trapezoid, and it is quite another other class of geometrical figures already.
For blondes helped to draw kria, author of blog kria-tiv.
 |
| Rectangular trapezoid |
A rectangular trapezoid always has two right angles. On a picture direct corners are marked little squares in tops A and D. Direct corners can be situated in two any contiguous tops of trapezoid.
 |
| Rectangular trapezoid |
On this picture of rectangular trapezoid direct corners are located in tops B and С.
In mathematics there is determination of rectangular trapezoid, which over is brought and in Wikipedia: the rectangular is name a trapezoid at which even one corner of line. This classic determination of rectangular trapezoid, bluntly rewritten from sacred mathematical books. In Euclidean geometry a rectangular trapezoid always has two lines of corner, as two sides trapezoids, called grounds, are parallel. Segment BC, formative a direct corner with founding of АВ, will be always perpendicular to the second founding of CD. With one or three direct corners there can be only a curvilinear rectangular trapezoid, and it is quite another other class of geometrical figures already.
For blondes helped to draw kria, author of blog kria-tiv.
Subscribe to:
Posts (Atom)