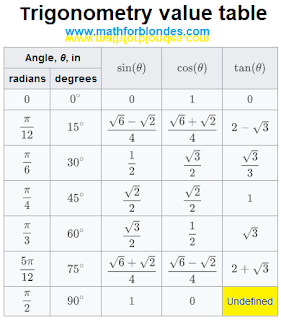
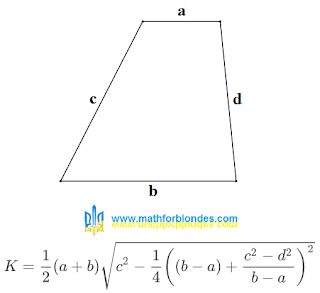
Annotation
Identical sums
 |
| Identical sums |
The number of sums in this group is determined by the number of terms. For infinite sums, it is equal to infinity.
Decomposition sums
 |
| Decomposition sums |
Any of these sums can be obtained by decomposing the result of addition into terms using linear angular functions. Having thus obtained two terms, any of them can also be decomposed into terms, and so on. An example expansion for the first three sums:
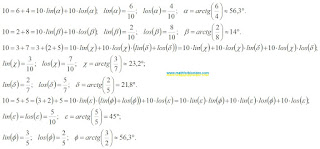 |
| Decomposing into terms |
An example of decomposing a number into three terms shows that different decomposition options can give the same sum, which underlies the associative properties of addition. The more terms the sum contains, the more different expansion options there can be. The expansion into terms can be continued indefinitely. Different angles and different decomposition algorithms make it possible to obtain different variants of infinite sums. The theory of limits allows you to determine the result of addition based on the analysis of terms. The expansion into terms allows the summation result to be represented as an infinite series of terms.
For example, let's decompose the unit into an infinite sum according to the following principle: the expansion is performed at an angle of 45°, each second term is decomposed into two terms.
 |
| Decomposition into an infinite number of terms |
The curly brackets indicate the sum of the invisible compensating group of terms, which complements the result of addition to an integer unit. It can be assumed that any sum, even an infinite divergent series, in trigonometric form is equal to one.
Other sums
Let's assume that for the sum a+b=c there is another addition result d that is not equal to c. That is, a+b=d. We represent these two expressions using linear angle functions, and then we translate them into a trigonometric form:
 |
| Different addition results |
The assumption that there are different addition results for the same sum takes us beyond the boundaries of mathematics, where the basic trigonometric relations stop working:
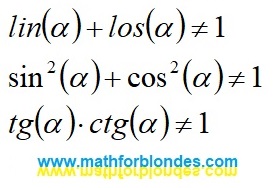 |
| Beyond the boundaries of mathematics |
Why can't the same sum of terms have two different addition results? You can understand this by considering the reverse process - the transformation of trigonometric functions into specific mathematical sums. I will cover this in more detail in a separate post.
In conclusion of the conversation about the presence of two different results of addition in divergent series, I will give an example from physics. In the earth's crust (convergent series) there are natural caves (the sum of the convergent series). Using special mechanisms (convergence according to Cesaro, etc.) we can get artificial tunnels (the sum of a convergent series). There are no natural caves in the seas and oceans (divergent series, the sum of the series is missing). The use of special mechanisms (convergence according to Cesaro, etc.) allows us to obtain artificial tunnels (the sum of a divergent series) in the water column. Based on this mathematically proven theory, it is possible to design a network of tunnels for roads and railways that encircle the entire earth's surface. Such a theory is quite possible if we do not understand the difference between solids (convergent series) and liquids (divergent series).