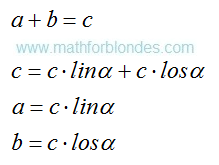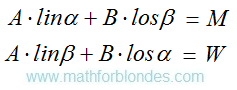Last time we considered the fine-molded engine which is used in our technique. The main shortcoming - they do not save the vehicle from influence of inertial forces. Our observations show that the UFO can instantly change speed, can turn at a huge speed at right angle. It breaks the fundamental law of physics - a law of inertia. We consider that it is impossible. If such flights are impossible, means and the UFO does not exist. Our such logic.
Whether it is possible to bypass laws of inertia, without breaking them? Of course. Let's consider the principle of operation non-inertial engine of the UFO. It is the engine of absolutely other type - volume action. This engine creates internal gravitational field of the variable direction and force in the UFO. Internal gravitational field of the UFO forms selfcontained space around its design. All device UFO is as if wrapped in a cocoon.
How we overcome inertial forces? We considered our
terrestrial engines earlier. In each car there are seat belts for overcoming an inertial force. Internal gravitational field of the UFO allows to overcome inertial forces at the atomic level. Each atom of a body of the extraterrestrial has the seat belt. The observer will think that inertial forces do not act on the UFO.
 |
| Non-inertial engine of the UFO |
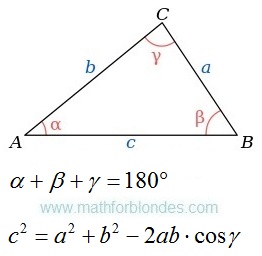
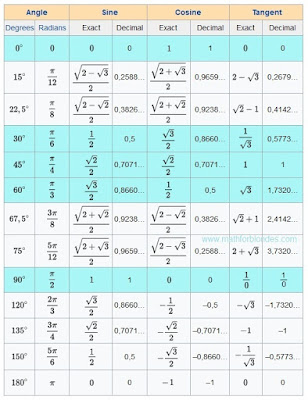
It is absolutely prime further and we know it long ago. If equally effective internal gravitational field of the UFO it is equal to the gravity operating on it, then the UFO not movably. If the common force is directed up at an angle, then you need the help of
trigonometry. It is a task from our, terrestrial, textbooks.
The crew of the UFO constantly is in an imponderability. The UFO constantly is in falling. For the UFO does not matter in what party and with what speed to fall. If to equip your car with the non-inertia gravitational engine, it will turn into the UFO. I do not recommend to leave limits of an Earth's atmosphere - the car housing is not calculated on it.
The UFOs non-inertial engines fall into a class of planetary engines, as well as our rocket engines. With their help it is possible to explore planets in star systems. Between star systems non-inertial engines are not suitable for travel. They have very small effectiveness on overcoming distances in space. For this purpose extraterrestrials use other type of driving - teleportation.
Why I speak about other type of driving here? The non-inertial engine and teleportation are based on one mathematical principle - the principle of closed space. In different engines different physical fields turn into closed space. The UFOs non-inertial engine closes gravitational field.
How to close space? Ask this question to our mathematicians. In reply we will hear infinitely sad song of magicians that in different sections mathematicians are different approaches to this question.
Our physicists and engineers took the first step on the way of use of physical fields for driving. In electric motors the principle of the rotating magnetic field is used. We use a magnetic levitation.
What else convinces me of reality of the UFO? Form of aircraft of extraterrestrials. You sometime heard about the cube flying in a palate? I did not hear too. Sense here not only in streamline shapes of the UFO. Physical fields have no right angles and polygonal lines.
I expect your question: if UFOs and extraterrestrials really fly over our planet, then why they do not come to us into contact? We will talk about it somehow another time.