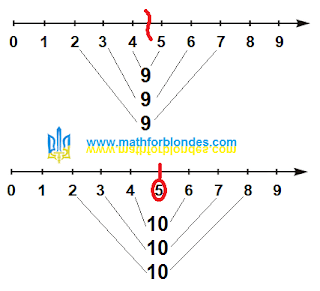
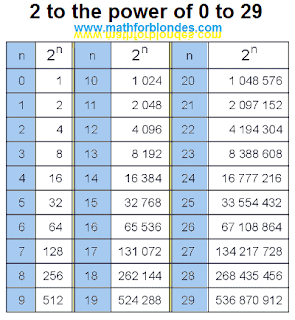
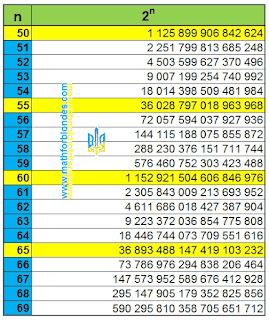
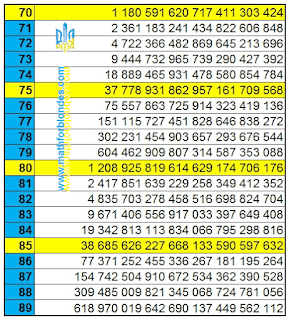
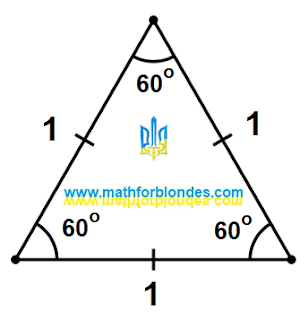
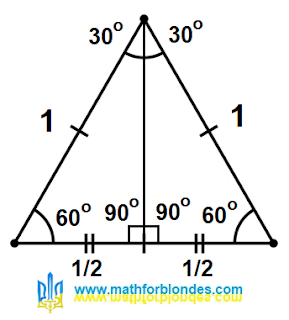
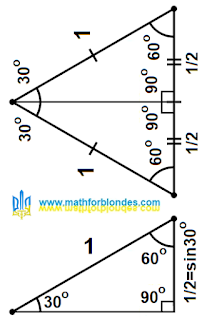
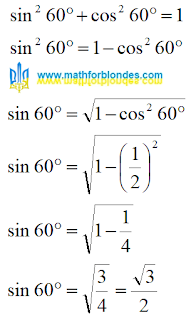|
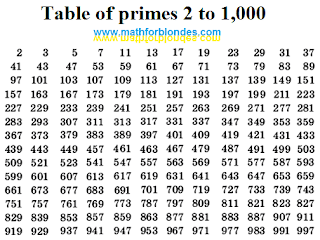
| Prime number X |
Elon Musk published the prime number X on . As you can see, this prime number actually has 1800 digits. Reddit users have started a fascinating discussion about this prime number. I liked these comments:
Watch out: there’s a sneaky 7 near the end of the tenth row.
It's pretty obvious someone tried a few tweaks until they found a configuration that actually gives a prime. But yeah, the digit 7 is the most visible one and surely the last change made - essentially that's the point where the author gave up on having a nicer solution :)
Now I'll remove all 1 from the drawing and we'll see what's left.
 |
| Prime number X without 1 |
As you can see, the number of eights in the lines does not correspond to the ideal pattern. And also this number 7. Yes, even Elon Musk is powerless against mathematics.
I’m interested in this question: how much money did Elon Musk pay for this work? Personally, I would not regret the largest amount possible. What could be greater than the SUM OF ALL NATURAL NUMBERS? Nothing. Who do I owe -$1/12? Why can you use this in physics, but you can’t pay for work?