Before we will pass to formulation of determinations of trigonometric functions with the use of portrait of tangent, we need to understand, what a trigonometric circle differs from all other circles. In reasoning we will use one mathematical focus sense of that is based exactly on these differences.
We will take the picture of circumference from determination of trigonometric functions. He looks here so.

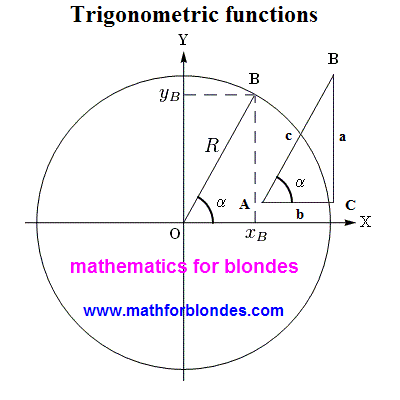
On a picture the ordinary circumference of arbitrary radius is represented. As in the center of circumference cheekily fell to pieces the cartesian coordinate system, then all points of this circumference have vertical and horizontal coordinates. Radius of circumference and coordinate of points expressed by numbers. The intersections of axes of coordinates and circumference are determined by the size of radius of circumference and numeral him equal to.
In an order to convert an ordinary circumference into trigonometric one, it is needed to divide all elements of circumference into the radius of circumference. Letters of "X" and "Y" are the tags of the system of coordinates, designating her obtrusive presence on our picture. These letters by a radius are not divided, as well as letter of "B", designating a point on a circumference. Point "0"(zero) as a result of dividing by a radius so will remain a point "0"(remember, the zero divided by any number equals a zero?). Corner alpha it is possible to divide into a number, but it is impossible to divide into a radius circumferences(by the way, here to you the prepared proof that a division does not make sense) :))), therefore a corner it is better not to touch, in order to avoid large troubles(from all present person on a picture, a corner is the steepest element, he is in all trigonometric functions in the natural kind). For us remain only radius of circumference and coordinate points of "B", that we can divide into the size of radius of circumference.
Clear that at dividing of radius of circumference by an exactly such radius, we will get unit as a result. And at dividing of coordinates of point of circumference by a radius we will get the values of sine and cosine of corner alpha(on determination of trigonometric functions). That is our transformations look on a picture.

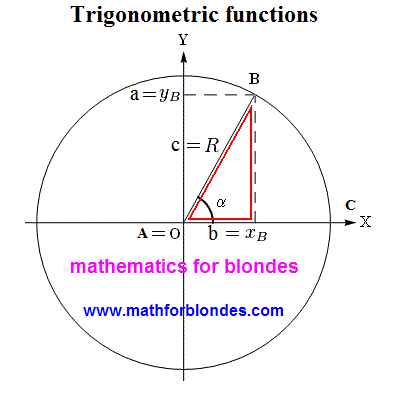
Now we need only to substitute all radiuses by units and coordinates of point on a sine and cosine of corner alpha and a trigonometric circumference will turn out for us. We even can set forth determination of single circumference (let child prodigy teach):
a circumference with a radius equal to unit is named a trigonometric circumference, if there is a center of the cartesian system of coordinates in the center of circumference.
This determination far not complete and does not take into account many nuances on that mathematicians take no notice usually. But about it we better will talk at the study of properties of trigonometric functions. And while we will look at a picture, as a trigonometric circumference looks in all beauty.
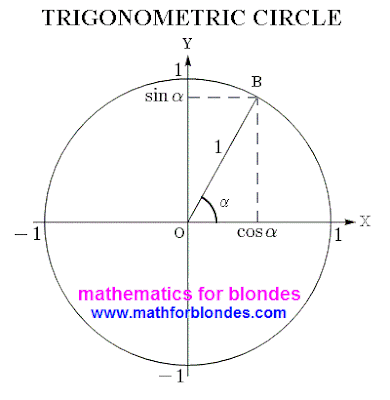
Actually, this is a trigonometric circle. If on him to place the values of different corners and corresponding to them values of sine and cosine, then we will get the trigonometric circle of sine and cosine.
Now about that focus that we will do during formulation of determinations of trigonometric functions. Here we substituted the radius of circumference by unit, and there we will act vice versa - we will replace unit the radius of circumference. Id est, from a trigonometric circumference to pass to the circumference of arbitrary radius, as that is required by a textbook on mathematics.