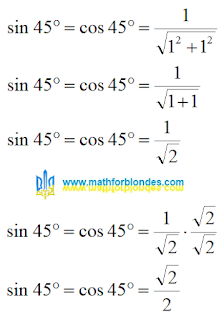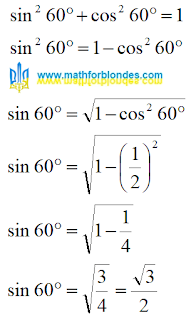-
Why is the sine of 30 degrees equal to half one?
What is the sine of 60 degrees?
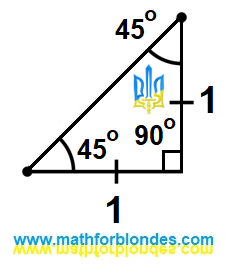
Sine and cosine of 45 degrees
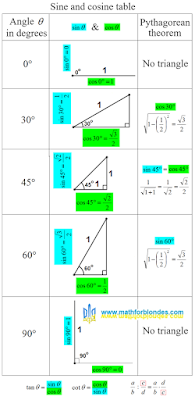 |
| Sine and cosine table |
The table indicates which sides of the triangle to take as a unit. For 0 and 90 degrees, triangles do not exist, these are ordinary segments.
The third column of the table shows how to use the Pythagorean theorem to calculate the desired value of the sine or cosine. For a cosine of 30 degrees and a sine of 60 degrees, the calculations are the same.
At the bottom of the table there are hints on how to calculate the tangent and cotangent values if you know the sine and cosine values. If you forgot how to divide one fraction by another, use one more hint. You need to multiply the first fraction by the reciprocal of the second fraction.