It's easy to remember the rules for multiplying or dividing positive and negative numbers. If two numbers have different signs, the result will always be a minus sign. If two numbers have the same sign, the result will always be a plus. Let's consider all possible options.
What gives plus for minus? When multiplying and dividing, plus by minus gives a minus.
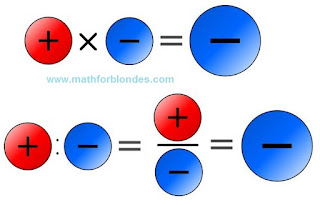 |
| What gives plus for minus? |
What gives a minus on plus? When multiplying and dividing, we also get a minus sign as a result.
 |
| What gives a minus on plus? |
As you can see, all the options for multiplying or dividing positive and negative numbers have been exhausted, but the plus sign has not appeared.
What gives a minus on a minus? There will always be a plus if we do multiplication or division.
 |
| What gives a minus on a minus? |
What gives plus for plus? It's quite simple here. Multiplying or dividing plus by plus always gives plus.
 |
| What gives plus for plus? |
If everything is clear with the multiplication and division of two pluses (the result is the same plus), then with two minuses, nothing is clear.
Why does a minus and a minus make a plus?
I can assure you that, intuitively, mathematicians have correctly solved the problem of multiplying and dividing the pros and cons. They wrote down the rules in textbooks without giving us any reasons. For the correct answer to the question, we need to figure out what the plus and minus signs mean in mathematics.
One mathematics teacher told us in the classroom: "Mathematics is an exact science, if you lie twice, you get the truth". This statement was very useful to me. Once I was solving a difficult problem with a long solution. I knew exactly what the result should be. But the result was different. I have been looking for an error in the calculations for a long time, but I could not find it. Then, a few steps before the final result, I changed one number so that the result was correct. I lied twice in the calculations and got the correct result. This is very similar to the minus on minus equals plus rule, isn't it?















No comments:
Post a Comment