Sine and cosine of 45 degrees

We have already considered what the sine of 30 degrees is and what the sine of 60 degrees is equal to. Now we will see how to find the sine and cosine of 45 degrees and why they are equal.

Last time we considered an equilateral triangle. Now we will consider an isosceles right triangle. A very rare beast in a herd of triangles. Mathematicians have known it for many thousands of years, and it is simply boring for mathematicians to tinker with it.

Isosceles right triangle

We will consider a tired isosceles right triangle. Why is the triangle tired? He lay down on his side to rest.

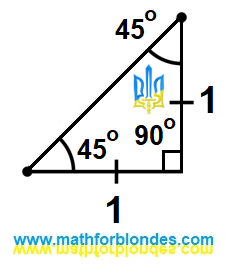Isosceles right triangle

The legs of this triangle are equal to one. Once again I repeat that both legs have the same length. We do not know the length of the hypotenuse of this triangle, but we can easily calculate it using the Pythagorean theorem.

Sine and cosine of 45 degrees

Smart people came to us and said that the sine and cosine of an angle are equal to the ratio of the legs to the hypotenuse. Since the legs of a right triangle with an angle of 45 degrees are equal, then the value of the sine of 45 degrees is equal to the value of the cosine of 45 degrees. We take the math in hand and calculate this value.

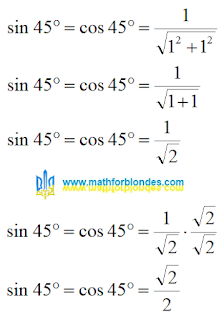Sine and cosine of 45 degrees

Why did I multiply the numerator and denominator of a fraction by the square root of two? Small children do not like lumps in porridge. Mathematicians don't like square roots in denominators. Very capricious uncles and aunts.