 |
| 2-spiral |
On a 2-spiral the main axis is formed by successive powers of the number 2. All odd numbers are located at the beginning of the numerical N-rays, all even numbers are located on the N-rays of the spiral.
On the 2.0-turn there is one single arc of size 360°, at the beginning of this turn there is the number 1. This is the only number spiral that has no other numbers other than one on the zero turn. The number of numbers and unit arcs is determined by formula (2).
The 2.1-turn is divided into two single arcs of size 180° and there are two numbers on it - 2 and 3. Here and on the remaining turns, the number of numbers and unit arcs is determined by formula (1).
 |
| Calculations for 2-spiral |
The 2.2-turn form four single arcs measuring 90°, on which the numbers 4, 5, 6, 7 are located. The number 6 is located on the continuation of the 3-ray.
The 2.3-turn form 8 single arcs measuring 45°. This turn contains numbers from 8 to 15 inclusive. The numbers 10, 12 and 14 are located on the continuation of the 5-ray, 3-ray and 7-ray respectively.
The further arrangement of natural numbers on the 2-spiral can be traced in the figure above.
3-spiral
 |
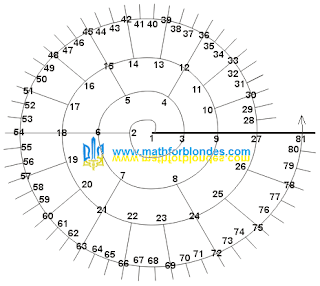| 3-spiral |
The main axis of the 3-spiral is formed by successive powers of the number 3. On the 3.0-turn there are two single arcs of size 180° and there are two numbers on it - these are 1 and 2 . The number of unit arcs and numbers is determined by formula (2).
The 3.1-turn is divided into six single arcs measuring 60°, on which the numbers 3, 4, 5, 6, 7 and 8 are located. The number of unit arcs and numbers is determined by formula (1). The number 6 is located on the continuation of the 2-ray and is the result of multiplying the number 2 by the number 3.
 |
| Calculations for 3-spiral |
The 3.2-turn is formed by eighteen single arcs of size 20°, on which the numbers 9 to 26 are located.
4-spiral
 |
| 4-spiral |
The main axis of the 4-spiral is formed by successive powers of the number 4. On the 4.0-turn there are three single arcs of size 120° and on it there are three numbers - 1, 2 and 3.
The 4.1-turn is divided into twelve single arcs measuring 30°.
 |
| Calculations for 4-spiral |
The 4.2-turn is divided into forty-eight unit arcs measuring 7.5°.
Each turn of the 4-helix contains two compressed turns of the 2-helix. Compression occurs unevenly and is determined by the structure of the zero turn of the 4-helix. Zero and even turns of the 2-helix are compressed to 1/3 turns of the 4-helix, the first and odd turns - to 2/3 . This uneven compression ensures that the single angular segments of all turns in the 4-helix structure are equal.
Similar uneven compression occurs on the remaining spirals, built on numbers equal to the power of the number a, greater than the first power. Thus, for an 8-helix (a=23), each turn of which contains three turns of a 2-helix, the proportions are equal: 1/7, 2/7, 4/7.
5-spiral
 |
| 5-spiral |
The main axis of the 5-helix is formed by successive powers of the number 5. On the 5.0-turn there are four single arcs of size 90° and on it there are four numbers - 1, 2, 3 and 4.
The 5.1-turn is divided into twenty single arcs measuring 18°.
 |
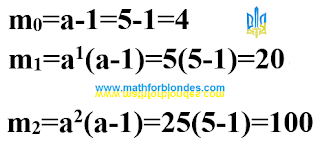| Calculations for 5-spiral |
The 5.2-turn is divided into one hundred unit arcs of size 3.6°.
In a similar way, you can build a number spiral for any natural number.
Continued: Analysis of number spirals.
Posts
No comments:
Post a Comment