Trapezoid
Once I already considered the formula for the diagonals of a trapezoid. When moving from a trapezoid to a rectangle, I ended up with an indefinite expression - zero divided by zero under the square root sign.
Now I propose to consider another formula. In the 7th century, the Indian mathematician Bhaskara I derived a formula for determining with successive sides a, b, c, d:
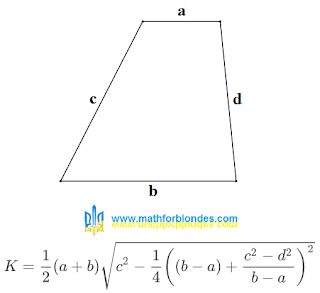 |
| Trapezoid and formula |
Rectangle
If you apply the conditions describing a rectangle to this formula, you can get a very interesting result of dividing zero by zero:
 |
| Formulas for converting a trapezoid into a rectangle |
Zero divided by zero equals zero. I am categorically against this result. Once I used a similar trick in another formula and it turned out that zero divided by zero is equal to one. I agree with this result. But. Never trust anyone, not even yourself, you can make mistakes too. Then I came up with the following idea.
The result of dividing zero by zero depends on the mathematical operation in which it occurs. When multiplying, the result is equal to one, when adding, the result is zero.
For the future, you will need to remember this and not be surprised by anything.
Parallelogram
Let's return to our formula for the area of a trapezoid. I remembered another geometric figure whose parallel sides are equal - this is a .
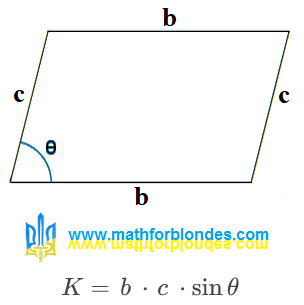 |
| Parallelogram and its area |
This formula contains the sine of the angle between the base of the parallelogram and its side. After transforming the formula for the area of a trapezoid, this factor is completely absent.
The formula for the area of a parallelogram is easily converted to the area of a rectangle. The sine of an angle of 90 degrees is equal to 1. The third factor in the formula for the area of a parallelogram disappears, we get the formula for the area of a rectangle.
Division by zero
Such an obvious bug in the formula for the area of a trapezoid suggests that it is strictly not recommended to consider the result of dividing zero by zero as correct. The formula for the area of a trapezoid can only be applied to a trapezoid and is not applicable beyond the boundaries of the trapezoid.
After some thought, I found a second option that confirmed my guess about the result of dividing zero by zero. We converted the formula for the area of a trapezoid into the formula for the area of a rectangle. After this, we can easily convert the formula for the area of a rectangle into the formula for the area of a parallelogram. Here's how it's done.
 |
| Converting the area of a rectangle to the area of a parallelogram |
Now everything has fallen into place. I take my hat off to the Indian mathematician who teaches us how to correctly understand division by zero.
Don't be afraid to test the math. You will find a lot of interesting things for yourself. Mathematics from a complex science will turn into an ordinary tool of knowledge for you.
In conclusion, I can repeat the conclusion from the previous article: cunning tricks of mathematicians can lead to false results. For an example, see my article “Permuting Addends in Infinite Sums”.
More interesting math ideas on the page "My Math"















No comments:
Post a Comment