Trigonometry and division by zero

Why was I so surprised by the result of dividing zero by zero when transforming the formula for the area of a trapezoid? In this article I will try to explain to you.

I have been studying trigonometry for a long time. The trigonometric transformations that I will show you now are for me somewhere at the foundation of mathematics. In those lost pages of mathematics textbooks that preceded natural numbers. Or that we have yet to write. A question for all of you: without understanding what could the very concept of counting not have arisen?

Trigonometry

This is a small lyrical digression for those mathematicians who have long forgotten trigonometry. What self-respecting mathematician would engage in such a long-known nonsense as trigonometry? I remind them especially for them:

Trigonometry formulas

Schoolchildren know these trigonometric formulas well. They have been tested by practical application for hundreds of years. Many generations of mathematicians have applied these trigonometric transformations without any problems. I have no reason to doubt the correctness of these trigonometric formulas.

But these formulas contain one small problem, the solution of which has proven beyond the capabilities of all generations of mathematicians. This problem is called "division by zero". Now we will see how it looks in trigonometric formulas.

Division by zero

Now we will substitute the values of trigonometric functions for different angle values into the given trigonometric formulas. No special problems arise in this case, except for angles equal to 0 and 90 degrees. Let's see what happens:

Trigonometry and division by zero

Trigonometric formulas clearly show that:

1. Dividing zero by zero results in one.

2. Dividing a number (one) by zero is possible.

Statement number 1 has been known to me for a long time. If the formulas given are algebra, then I have no problems with the geometric and physical meaning of dividing zero by zero. Perhaps I have already written about this. I don't remember. If I haven't, I will.

For a long time I didn't believe in the possibility of dividing a number by zero. I recently solved this problem. Now I need to format it nicely and publish it. Unfortunately, all my time is taken up with earning money for a living, and not with solving mathematical problems.

By the way, I have believed in the possibility of division by zero for a very long time. It was this belief that made me take up trigonometry. I did not know trigonometry either at school or at the institute. It is the understanding of trigonometry that allows you to find a solution to the problem of division by zero. It is enough to know what and where to look for. You already know what to look for. Where to look, I will soon show you along with the basic principles of division by zero.

The order of performing mathematical operations
and the result of division by zero

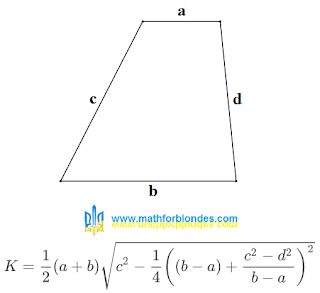
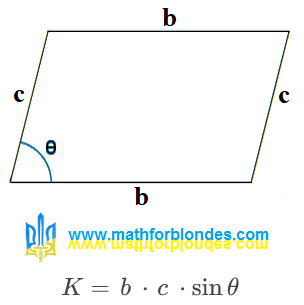
Now let's get back to the little problem that dividing zero by zero has different results in different formulas: in trigonometric formulas and in the formula for transforming the area of ​​a trapezoid. It is quite possible that the result depends not on the mathematical operations, but on the order in which the multiplication and division are performed.

Let me remind you that according to the rules of mathematics, multiplication and division are performed in the order in which they are written in a mathematical expression. Who writes down a mathematical expression? A mathematician. On what basis? Now that's an interesting question. Ideally, the order of mathematical operations should be determined by the physical process that the mathematical expression describes. In fact, the mathematician will write them down in whatever order he wants. But let's see what I mean:

Mathematical operations and division by zero

In my opinion, this option fits better into the mathematical rules. But the determining factor will be the result of practical application of these theories in the future. Why did I designate the result of dividing one by zero as "x"? Whatever it is, as a result of multiplying by zero we get zero.

Conclusions

I have neither moral nor legal right to make authoritative statements. I have neither authority nor mathematical education and I have nothing to do with mathematics. Mathematics is my hobby. But this is my main advantage. I can say whatever I consider necessary. No one will kick me out of school or work for this. Therefore, as a rational being, I will tell you the following.

Mathematicians are absolutely right when they say that division by zero is impossible. Within the framework of number theory, no one has been able to solve this problem and is unlikely to be able to. Set theory has nothing to do with mathematics at all. What other tools do mathematicians have to solve the problem of division by zero? Geometry? Or something else?

I believe that the main mistake of mathematicians is their global approach to solving problems. Mathematicians always generalize and expand everything. The correct scientific approach also implies the ability to separate and narrow. Without this, science turns into a mediocre religion. Modern mathematicians are not even able to count the terms with their fingers when rearranging the terms in a sum. So what if this sum is infinite? The laws of mathematics are always the same for everyone. I still have many questions for mathematicians like "Why exactly this way and not otherwise?" I hope I will have time to formulate them.

More interesting math ideas on the page "My Math"

Area of a trapezoid and division by zero

Trapezoid

Once I already considered the formula for the diagonals of a trapezoid. When moving from a trapezoid to a rectangle, I ended up with an indefinite expression - zero divided by zero under the square root sign.

Now I propose to consider another formula. In the 7th century, the Indian mathematician Bhaskara I derived a formula for determining the area of a trapezoid with successive sides a, b, c, d:

Trapezoid and formula

Rectangle

If you apply the conditions describing a rectangle to this formula, you can get a very interesting result of dividing zero by zero:

Formulas for converting a trapezoid into a rectangle

Zero divided by zero equals zero. I am categorically against this result. Once I used a similar trick in another formula and it turned out that zero divided by zero is equal to one. I agree with this result. But. Never trust anyone, not even yourself, you can make mistakes too. Then I came up with the following idea.

The result of dividing zero by zero depends on the mathematical operation in which it occurs. When multiplying, the result is equal to one, when adding, the result is zero.

For the future, you will need to remember this and not be surprised by anything.

Parallelogram

Let's return to our formula for the area of a trapezoid. I remembered another geometric figure whose parallel sides are equal - this is a parallelogram.

Parallelogram and its area

This formula contains the sine of the angle between the base of the parallelogram and its side. After transforming the formula for the area of a trapezoid, this factor is completely absent.

The formula for the area of a parallelogram is easily converted to the area of a rectangle. The sine of an angle of 90 degrees is equal to 1. The third factor in the formula for the area of a parallelogram disappears, we get the formula for the area of a rectangle.

Division by zero

Such an obvious bug in the formula for the area of a trapezoid suggests that it is strictly not recommended to consider the result of dividing zero by zero as correct. The formula for the area of a trapezoid can only be applied to a trapezoid and is not applicable beyond the boundaries of the trapezoid.

After some thought, I found a second option that confirmed my guess about the result of dividing zero by zero. We converted the formula for the area of a trapezoid into the formula for the area of ​​a rectangle. After this, we can easily convert the formula for the area of a rectangle into the formula for the area of ​​a parallelogram. Here's how it's done.

Converting the area of a rectangle to the area of a parallelogram

Now everything has fallen into place. I take my hat off to the Indian mathematician who teaches us how to correctly understand division by zero.

Don't be afraid to test the math. You will find a lot of interesting things for yourself. Mathematics from a complex science will turn into an ordinary tool of knowledge for you.

In conclusion, I can repeat the conclusion from the previous article: cunning tricks of mathematicians can lead to false results. For an example, see my article “Permuting Addends in Infinite Sums”.

More interesting math ideas on the page "My Math"

Number spirals and prime numbers

Number spirals and prime numbers

https://doi.org/10.5281/zenodo.15024975

Beginning: Number spirals introduction

All primes of the form P are located at the beginning of the number rays on all number spirals, with the exception of the prime number a, located on the main axis of the a-spiral. The relative position of the prime numbers will change depending on the number a, which underlies the construction of the spiral. The arrangement of prime numbers on different number spirals is shown in the pictures below.

Prime numbers on a 2-spiral

Prime numbers on a 3-spiral

Prime numbers on a 4-spiral

Prime numbers on a 5-spiral

Composite numbers are on the rays of spirals built on numbers that are divisors of these numbers. On the remaining spirals they are located at the beginning of the number rays. For example, the number 6 is located on the continuation of the 3-ray 2-spiral and is the result of multiplying the number 3 by the number 2 . The same number 6 is located on the continuation of the 2-ray 3-spiral and is the result of multiplying the number 2 by the number 3 .

Consideration of number spirals will be continued in subsequent publications.

Number spirals and numeral systems

Number spirals and numeral systems

https://doi.org/10.5281/zenodo.15024975

Beginning: Number spirals introduction

Numbers on number spirals can be represented in different number systems. For example, consider the numbers on the main axis of some spirals in different number systems. Table 1 shows the numbers on the main axis of the 2-spiral in binary, decimal and hexadecimal numeral systems.

Main axis of 2-spiral

Table 2 presents the numbers on the main axis of the 10-spiral in the same numeral systems.

Main axis of 10-spiral

Similarly, Table 3 presents the numbers on the main axis of the 16-spiral.

Main axis of 16-spiral

As can be seen from the tables above, each a-spiral in the number system with the base a will consist of separate turns with numbers that have the same number of digits in the positional system. Each subsequent turn of the numerical spiral for the number a in the number system with the base a adds one digit in the positional system. Each n-turn consists of numbers written using n+1 number of digits.

If we introduce the rule that unit arcs on one turn must be of the same length, then the number spiral will turn into a set of concentric circles. Each circle will contain numbers with the same number of digits. The introduction of such a rule violates the visual continuity of natural numbers.

Thus, each a-spiral is a graphical representation of natural numbers in the numeral system with the base a, which is written in the numeral system we have chosen. By default we use the decimal numeral system.

Continued: Number spirals and prime numbers.

Analysis of number spirals

Analysis of number spirals

https://doi.org/10.5281/zenodo.15024975

Beginning: Number spirals introduction

Movement along the turns of any a-helix is an addition table with the sequential addition of one unit to the previous number, starting from one. Movement along the rays of any a-spiral is a multiplication table with sequential multiplication of the number located at the beginning of the ray by the number a. These two movements are perpendicular, indicating the fundamental difference between addition and multiplication.

If we draw the axis of symmetry through the main axis of any a-spiral, then the symmetrical numbers on the turns form decomposition sums. For any a.n-turn this decomposition sum is equal to aⁿ+aⁿ⁺¹. As an example, the decomposition sums are shown in 4.1-turn. The number of such sums, taking into account the sum of the numbers aⁿ and aⁿ⁺¹ on the main axis, is equal to m_n/2.

Decomposition sums

This property of number spirals allows you to calculate the sum of natural numbers located on one a.n-turn. To do this, you need to multiply the sum of the decomposition by the number of such sums using formula (1), add a number located on the axis of symmetry, which is equal to half the sum of the decomposition, and subtract the number aⁿ⁺¹, which refers to the following turn:

Sum of numbers on a turn

Formula (3) allows us to derive the long-known formula for determining sums of all natural numbers from one to any number a. To do this, you need to determine the sum of the numbers on the zero turn of the a-spiral and add the number itself a:

Sum of natural numbers

If we construct a number spiral for an infinitely large number (∞-spiral), the beginning of this spiral will differ from the number ray only in the absence of zero. The zero turn will consist of an infinitely large number of unit arcs, each unit arc will be limited by rays with an infinitely small angle value. The curvature of the coil will begin to appear in the region of very large numbers from the beginning of the spiral.

Continued: Number spirals and numeral systems.

Description of number spirals

Description of number spirals

https://doi.org/10.5281/zenodo.15024975

Beginning: Number spirals introduction.

2-spiral

2-spiral

On a 2-spiral the main axis is formed by successive powers of the number 2. All odd numbers are located at the beginning of the numerical N-rays, all even numbers are located on the N-rays of the spiral.

On the 2.0-turn there is one single arc of size 360°, at the beginning of this turn there is the number 1. This is the only number spiral that has no other numbers other than one on the zero turn. The number of numbers and unit arcs is determined by formula (2).

The 2.1-turn is divided into two single arcs of size 180° and there are two numbers on it - 2 and 3. Here and on the remaining turns, the number of numbers and unit arcs is determined by formula (1).

Calculations for 2-spiral

The 2.2-turn form four single arcs measuring 90°, on which the numbers 4, 5, 6, 7 are located. The number 6 is located on the continuation of the 3-ray.

The 2.3-turn form 8 single arcs measuring 45°. This turn contains numbers from 8 to 15 inclusive. The numbers 10, 12 and 14 are located on the continuation of the 5-ray, 3-ray and 7-ray respectively.

The further arrangement of natural numbers on the 2-spiral can be traced in the figure above.

3-spiral

3-spiral

The main axis of the 3-spiral is formed by successive powers of the number 3. On the 3.0-turn there are two single arcs of size 180° and there are two numbers on it - these are 1 and 2 . The number of unit arcs and numbers is determined by formula (2).

The 3.1-turn is divided into six single arcs measuring 60°, on which the numbers 3, 4, 5, 6, 7 and 8 are located. The number of unit arcs and numbers is determined by formula (1). The number 6 is located on the continuation of the 2-ray and is the result of multiplying the number 2 by the number 3.

Calculations for 3-spiral

The 3.2-turn is formed by eighteen single arcs of size 20°, on which the numbers 9 to 26 are located.

4-spiral

4-spiral

The main axis of the 4-spiral is formed by successive powers of the number 4. On the 4.0-turn there are three single arcs of size 120° and on it there are three numbers - 1, 2 and 3.

The 4.1-turn is divided into twelve single arcs measuring 30°.

Calculations for 4-spiral

The 4.2-turn is divided into forty-eight unit arcs measuring 7.5°.

Each turn of the 4-helix contains two compressed turns of the 2-helix. Compression occurs unevenly and is determined by the structure of the zero turn of the 4-helix. Zero and even turns of the 2-helix are compressed to 1/3 turns of the 4-helix, the first and odd turns - to 2/3 . This uneven compression ensures that the single angular segments of all turns in the 4-helix structure are equal.

Similar uneven compression occurs on the remaining spirals, built on numbers equal to the power of the number a, greater than the first power. Thus, for an 8-helix (a=2³), each turn of which contains three turns of a 2-helix, the proportions are equal: 1/7, 2/7, 4/7.

5-spiral

5-spiral

The main axis of the 5-helix is formed by successive powers of the number 5. On the 5.0-turn there are four single arcs of size 90° and on it there are four numbers - 1, 2, 3 and 4.

The 5.1-turn is divided into twenty single arcs measuring 18°.

Calculations for 5-spiral

The 5.2-turn is divided into one hundred unit arcs of size 3.6°.

In a similar way, you can build a number spiral for any natural number.

Continued: Analysis of number spirals.

Number spirals

Number spirals

https://doi.org/10.5281/zenodo.15024975

Beginning: Number spirals introduction

If you use angle units of measurement and an arbitrary spiral to visually display natural numbers, then all numbers can be ordered according to the following rules:

1. On the main axis of the a-spiral there are numbers of the form aⁿ in ascending order, where а>1, n≥0.

2. The main axis coincides with the zero ray of angle units of measurement and has the following form:

The main axis of the number spiral

3. The main axis divides the spiral into separate turns measuring 360°, which are appropriately numbered according to the exponent of the number a located at the beginning of each turn. For example, a.0-turn, a.1-turn, a.n-turn. The distance between the turns of the spiral is arbitrary.

4. Each turn of the a-spiral is divided by rays into an equal number of single angular sectors, which divide the turn into single arcs. Each unit arc has an arbitrary length and corresponds to one numerical unit. Unit arcs separate two adjacent natural numbers, which are located at the intersections of rays and turns of the spiral.

5. The number of unit sectors and the number of natural numbers m_n for each a.n-turn is determined by formula (1).

6. For zero turns of all a-spirals the number of unit sectors and natural numbers is determined by formula (2).

Number spirals formulas

7. Each unit arc from a turn m_n is divided into a unit arcs on the next turn m_n+1 with new rays.

8. At the beginning of each ray (N-ray), at the intersection with the turn, there is a natural number N of the form P_a , prime with respect to the number a.

9. On the continuation of the N-rays, at the points of intersection with subsequent turns, there are natural numbers that are multiples of the number a, forming the main axis of the a-spiral.

Continued: Description of number spirals.