Terminating trigonometric functions

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Three main types of trigonometric functions

Lesson 4

TERMINATING TRIGONOMETRIC FUNCTIONS

The sine and cosine are rather well studied, their values cannot be more unit. If to divide elements of a rectangle into length of diagonal, lengths of the parties will accept values of a sine and a cosine. Also the parties of a rectangle are diagonal projections in the perpendicular directions.

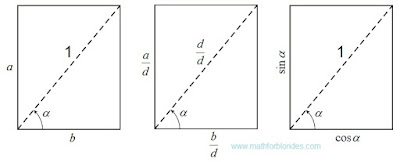Sine and cosine

Names of all trigonometric functions depend on the line of the beginning of measurement of a angle. The same line defines the direction of projection. Dependence between legs and a hypotenuse in a rectangular triangle, known as "Pythagorean theorem" (for length units of measure, not the bound to a hypotenuse) or "Pythagorean trigonometric identity" (when hypotenuse length is accepted to a unit of measure of length), is an integral part of properties of a rectangle.

If we project simple diagonal on the parties of a rectangle, then we will receive two projections of diagonal expressed through different angles. If we project the same parties on diagonal, then we will receive the diagonal length as the sum of two projections of the parties.

Pythagorean trigonometric identity

The Pythagorean theorem is a dependence between diagonals and the parties of a rectangle.

At the following lesson we will consider
The infinite trigonometric functions