Trigonometric functions in a rectangle

Published on 7 July, 2016
"The Papers of Independent Authors"
Volume 36 of p. 46-69

Annotation

Representation of trigonometric functions in a rectangle allows to unite algebra, geometry and physics in a single whole.

Short analysis of trigonometric functions

Usually trigonometric functions of plane angle are defined in a rectangular triangle as ratios of the parties of this triangle [a reference to the source in the printing edition].

Trigonometric functions in a triangle

If to accept the definitions of trigonometric functions entered by mathematicians in a rectangular triangle, then values of these functions depend only on a ratio of the sizes of the parties of a triangle. The size of angles in a rectangular triangle is in the range of trigonometrical angles. Trigonometric functions have no signs and do not possess periodic. These properties are homocentrism elements.

The homocentrism mathematics is a mathematics in which the result depends on the option of the relative mathematics accepted by us or on our opinion. Striking examples of a homocentrism in mathematician are: division of numbers on positive and the negative, decimal numeration, numbers and inverse numbers, Cartesian coordinate system, etc.

In Cartesian coordinate system trigonometric functions are defined as coordinates of points of a unit circle [a reference to the source in the printing edition].

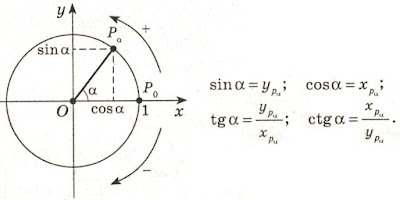Trigonometric functions in Cartesian coordinate system

This definition is possible only because for any point of a circle of coordinate are used as padding elements for creation of a rectangular triangle. For cross points of a circle and coordinate creation of a triangle is impossible.

For any point of the plane in Cartesian coordinate system trigonometric functions can be defined as the relation of coordinates of this point or the relation of coordinates of a point to distance from a point to the center of a frame. An exception is the cross point of coordinate (the center of a frame) for which trigonometric functions cannot be defined. This fact is congenital defect of Cartesian coordinate system. If it is necessary to define trigonometric functions for the point coinciding with the center of a frame, then the frame needs to be displaced aside.

In Cartesian coordinate system trigonometric functions are the relative and depend on the relative positioning of the plane on which the considered points, and frames are located. Periodicity of trigonometric functions is result of rotation of a piece around the center of a frame. Signs of trigonometric functions depend on the positive direction of coordinate accepted by us. All this result homocentrism of views of trigonometric functions.

Signs of trigonometric functions "+" and "-" serve for orientation in space of Cartesian coordinate system. In mathematical formulas with use of trigonometric functions, the sign "minus" at function automatically changes addition for a subtraction or a subtraction on addition. In formulas it is possible to do without the negative values of trigonometric functions. It will allow to reduce twice amount of values of trigonometric functions, but will increase quantity of formulas.

At the following lesson we will consider
Transformations of a triangle to a rectangle

More interesting math ideas on the page "My Math"