Trigonometry value table for children
 |
| Trigonometry value table |
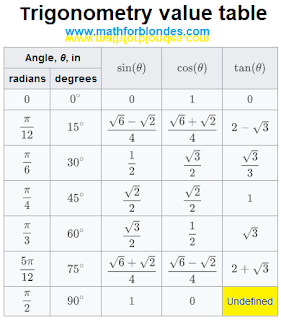
Why is this table of trigonometry values for kids (and mathematicians)? Firstly, the values of trigonometric functions are not given in numerical form, but in the form of mathematical expressions using square roots. Secondly, in this table it is indicated that the tangent of 90 degrees is undefined (I specially highlighted this cell in yellow).
The value of the tangent of 90 degrees is determined very simply, but mathematicians, as well as small children, do not understand what this means.
Division by zero
 |
| Division by zero |
The tangent of 90 degrees is equal to one divided by zero. That's what the math says. To understand division by zero, you need to know mathematics much better than we know it. If you firmly believe that zero is a number, you will never understand division by zero. Here you can find some of my publications on mathematics, which are somehow related to division by zero.
Division by zero can be found in various places in mathematics: the sine theorem, the equation of the straight line y=kx and so on. I suggest you explore these formulas on your own. Write about your results in the comments. If necessary, I will show you under what conditions division by zero appears there.
What is division by zero, I will definitely tell you in the future. But before that, there will be many more interesting things.
Trigonometry value table for engineers

| Trigonometry value table for engineers |
Division by zero is not as important for engineers as it is for physicists. Mathematicians have learned to bypass problem areas in engineering calculations. But physicists in their theories can meet division by zero much more often. If you already want to know what is the result of division by zero in your theoretical research, write in the comments, I will try to help you.















So what is the result of division by zero in theoretical research?
ReplyDeleteThe result of division by zero is a small shock. And it is not at all where mathematicians can look for it.
Delete