So, we will think of the simplest child's task about dogs and cats: "Now in zoosalone 2 cats 3 dogs clipped their wool. While 4 cats and 5 dogs are waiting in the queue. So how many cats and dogs want to change their image?" Simple task on two independent mathematical actions: add up the cats to the cats, add up the dogs to the dogs and get the result two numbers. One of which is the number of the cats, and the second the number of the dogs. That is simply. Now we will solve this task with the use of the matrix numbering on the calculator matrices.
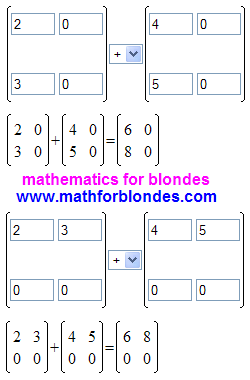
Here's what happened. As creators of calculator consider that operations with row vectors and column vectors are too primitive for mathematical knowledge of such high level, I had to go to a trick. The missing elements of square matrix the second order (this is the minimum size for the calculator matrices) I replaced with zeros.
On a picture it is shown that, I decided this task two methods: first, the values were in the first column, and then I put the same values in the first row of the matrix. Both variants gave the right result. From this we can conclude that the mathematical matrix operations within the meaning of a concurrent execution of mathematical operations with variables that have different units of measure.
In drawing up the matrix to solve a system of linear equations as a unit of measurement to take a unknown. For example, a unit of the decimal number system (just a number, the constant term of the equation), x, y, z, XXL ... Oh! It not from here, this unit is used to measure blouses. By the way, if you write in a matrix the number of your blouses, the matrix of this does not hurt - it does not matter what or where you are writing. But the correct solution to a system of equations with the matrix in the blouse you have not come out.
The principle of a matrix of equations for you take the numerical coefficients before unknown and inscribe them each into the place. That is where the matter of what and where exactly do you fit into the matrix. Then the resulting matrix solving.
Where is yet used principle of mathematical operations with matrices? When you count a whole bunch of money in paper notes and coins. Laid out bills and coins into piles on the dignity and recalculate the number in each pile. On this matrix method ends, farther you bring the got results to a single unit of measurement. Naturally, performing similar actions in everyday life, we never think about how it can be described mathematically.
Remember, we talked about the meters and decimetres? About bows and flounces, on a multi-core processor? There also can be used matrix methods of addition and subtraction. Perform all actions with the same unit of measurement, then all of the other unit of measurement. In the end, if necessary, make conversion between different units of measurement to another.
This method is very good to use in geodesy, when you need to add or subtract a large number of angles in degrees, minutes, seconds. Doing all the actions in degrees, then a minute, then with seconds. And then all received converting seconds into minutes and seconds. To obtain the minute add or subtract those moments obtained after converting seconds. Convert the result to degrees and minutes. To add on the total number of degrees degrees of minutes. All you have turned a corner in degrees, minutes, seconds.
I hope this article will be useful in practice, and you're using methods of matrix computations is in full knowledge of what you are doing and what the result will get.















No comments:
Post a Comment