sin x = -0.8453
On the table of sines we find the value of corner in degrees and minutes for x, equal +0.8453. This corner is in limits from 0 to 90 degrees and equal 54 degrees 42 minutes.
sin a = +0.8453
a = 57 degrees 42 minutes
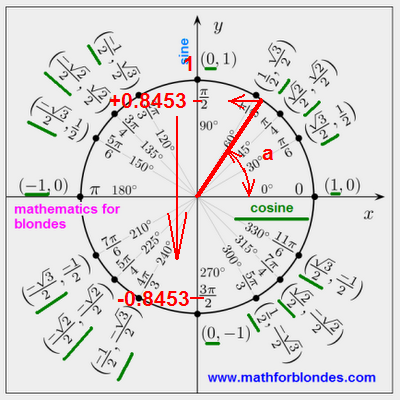
Farther we look a trigonometric circle and find a corner a. The positive values of sine are located in the overhead half of circle, negative values will be situated in the underbody of trigonometric circle.
One value of sine always has two values of corner. We will find these corners for the negative value of sine.
The first corner we will get, if to the corner a we will add 180 degrees. The second corner we will get, if from 360 degrees we will take away a corner a.
x1 = 180 degrees + a
x1 = 180 degrees + 57 degrees 42 minutes
x1 = (180 + 57) degrees 42 minutes
x1 = 237 degrees 42 minutes
x2 = 360 degrees - a
x2 = 360 degrees - 57 degrees 42 minutes
x2 = 359 degrees 60 minutes - 57 degrees 42 minutes
x2 = (359 - 57) degrees (60 - 42) minutes
x2 = 302 degrees 18 minutes
This was explanation, how to find a sine x with minus. Now a decision needs to be written down in accordance with bureaucratic rules that I do not know. It looks approximately so.
sin x = -0.8453
x = arcsin (-0.8453)
x1 = 237 degrees 42 minutes
x2 = 302 degrees 17 minutes
Posts
No comments:
Post a Comment