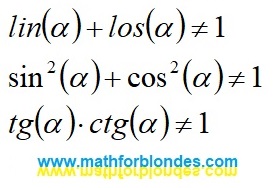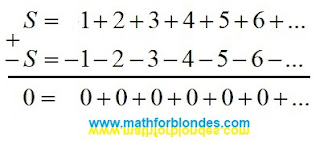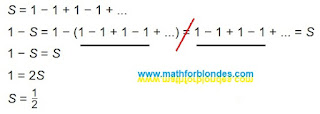Where does math end?

I was offered to sell my Russian site for 45.000 rubles. This prompted me to a very interesting question: "Where does mathematics end?". And here's my answer: "Math ends where money begins". Try any mathematical theory to apply to money and you will learn a lot of interesting things about this theory.

I love math trolling. The sentence contained the phrase: "The price may be revised upwards". My response was: "$45.000 Price may be revised down". From the point of view of mathematics, the equality 45.000=45.000 is beyond doubt. As soon as I add different units of money to this equality, it disappears.

Where does math end?

We use numbers to measure money. Numbers are written on coins and banknotes. Have you heard of banknote or a coin with the number "zero"? Zero is not a number. The more I study this question, the more I am convinced of the correctness of my statement.

Zero dollars

I'm not even talking about the minus sign on money. Through the prism of money, I considered set theory. The result is very interesting.

Why is the sine of 30 degrees equal to 1/2?

The answer to the question "why is the sine of 30 degrees equal to 1/2?" can be searched in the history of mathematics. These are ancient Mesopotamia, ancient Greece and other ancient civilizations. I am not an expert in this area. Obviously, knowledge has evolved from simpler to more complex. I will show you the most obvious answer to this question as I see it.

Equilateral triangle

Equilateral triangle

I have drawn an equilateral triangle with sides equal to one. I so want. The sum of the angles of a triangle is 180 degrees. An equilateral triangle has three 60 degree angles. I don't know trigonometry yet.

Height of an equilateral triangle

Height of an equilateral triangle

I drew the height in an equilateral triangle. The height is always perpendicular to the base of the triangle. If the height is drawn through the vertex of such a triangle, it will divide it into two equal right-angled triangles. This is always the case in isosceles triangles. An equilateral triangle is a special case of an isosceles triangle, in which the base is equal to the sides.

What happened as a result? The height divided the angle at the apex into two equal angles 60=30+30, it divided the base into two equal segments 1=(1/2)+(1/2). I still haven't heard anything about trigonometric functions.

Sine 30 degrees

After that, someone came up with trigonometric functions. I was told that the sine of an angle in a right triangle is the ratio of the opposite leg to the hypotenuse. How do I find the sine value for a 30 degree angle? I just flip the picture 90 degrees and remove all unnecessary.

Sine 30 degrees

The hypotenuse is equal to one. Any number divided by one does not change. So the length of the opposite leg in my triangle is equal to the sine of the angle of 30 degrees, that is, 1/2.

Cosine 30 degrees

The cosine of 30 degrees I can easily find from the Pythagorean theorem. We take the Pythagorean theorem in our hands and count.

Cosine 30 degrees

The cosine of 30 degrees turned out to be equal to the square root of three, divided by two.

Here's how easy it is to calculate. No tables needed.

Sums classification

Annotation

If you take any sum, then all other sums can be divided into three groups: identical sums, decomposition sums, and other sums. The classification criteria are the terms and the result of the addition.

Identical sums

Identical sums are combined into a separate group by the commutativity property. Sums from this group have pairwise identical terms and an equal number of terms. The result of adding these sums is the same. Here is an example of identical sums.

Identical sums

The number of sums in this group is determined by the number of terms. For infinite sums, it is equal to infinity.

Decomposition sums

If the results of adding a different number of terms or terms of different sizes are the same, then such sums form a decomposition group.

Decomposition sums

Any of these sums can be obtained by decomposing the result of addition into terms using linear angular functions. Having thus obtained two terms, any of them can also be decomposed into terms, and so on. An example expansion for the first three sums:

Decomposing into terms

An example of decomposing a number into three terms shows that different decomposition options can give the same sum, which underlies the associative properties of addition. The more terms the sum contains, the more different expansion options there can be. The expansion into terms can be continued indefinitely. Different angles and different decomposition algorithms make it possible to obtain different variants of infinite sums. The theory of limits allows you to determine the result of addition based on the analysis of terms. The expansion into terms allows the summation result to be represented as an infinite series of terms.

For example, let's decompose the unit into an infinite sum according to the following principle: the expansion is performed at an angle of 45°, each second term is decomposed into two terms.

Decomposition into an infinite number of terms

The curly brackets indicate the sum of the invisible compensating group of terms, which complements the result of addition to an integer unit. It can be assumed that any sum, even an infinite divergent series, in trigonometric form is equal to one.

Other sums

If the result of adding any amount differs from the result of adding the amount in question, then this amount has nothing to do with the amount in question and belongs to the “other sums” group.

Let's assume that for the sum a+b=c there is another addition result d that is not equal to c. That is, a+b=d. We represent these two expressions using linear angle functions, and then we translate them into a trigonometric form:

Different addition results

The assumption that there are different addition results for the same sum takes us beyond the boundaries of mathematics, where the basic trigonometric relations stop working:

Beyond the boundaries of mathematics

Why can't the same sum of terms have two different addition results? You can understand this by considering the reverse process - the transformation of trigonometric functions into specific mathematical sums. I will cover this in more detail in a separate post.

In conclusion of the conversation about the presence of two different results of addition in divergent series, I will give an example from physics. In the earth's crust (convergent series) there are natural caves (the sum of the convergent series). Using special mechanisms (convergence according to Cesaro, etc.) we can get artificial tunnels (the sum of a convergent series). There are no natural caves in the seas and oceans (divergent series, the sum of the series is missing). The use of special mechanisms (convergence according to Cesaro, etc.) allows us to obtain artificial tunnels (the sum of a divergent series) in the water column. Based on this mathematically proven theory, it is possible to design a network of tunnels for roads and railways that encircle the entire earth's surface. Such a theory is quite possible if we do not understand the difference between solids (convergent series) and liquids (divergent series).

Conclusion

There are no mathematical methods that allow you to get a different addition result for the sum in question.

Shift in arithmetic

Annotation

The use of a shift in arithmetic leads to the addition of terms with different units of measurement.

Consider the results of a shift in arithmetic addition. A shift is possible when performing addition in a column. For example, let's take a three-digit number and add to it the same number without a shift, with a shift by one position and with a shift by two positions. At the same time, we will observe the rule adopted when shifting infinite series - we discard the numbers of the second term that go beyond the boundaries of the first number.

Addition with a shift in a column

Shifting by a different number of positions leads to different results in the same way as when shifting infinite series. You can write the same expressions in a line with the subsequent indication of the units of measurement for each of the terms.

Addition with a shift in a line

Conclusion

The shift leads to a change in the unit of measurement of the shifted term. The shift is a violation of the basic law of addition - you cannot add terms with different units of measurement.

Trigonometry value table

Trigonometry value table for children

In trigonometry value table lists the sines, cosines, and tangents of multiples of 15 degrees from 0 to 90 degrees.

Trigonometry value table

Why is this table of trigonometry values for kids (and mathematicians)? Firstly, the values of trigonometric functions are not given in numerical form, but in the form of mathematical expressions using square roots. Secondly, in this table it is indicated that the tangent of 90 degrees is undefined (I specially highlighted this cell in yellow).

The value of the tangent of 90 degrees is determined very simply, but mathematicians, as well as small children, do not understand what this means.

Division by zero

By definition the tangent of 90 degrees is equal to the sine of 90 degrees divided by the cosine of 90 degrees. Let's take a look at the result.

Division by zero

The tangent of 90 degrees is equal to one divided by zero. That's what the math says. To understand division by zero, you need to know mathematics much better than we know it. If you firmly believe that zero is a number, you will never understand division by zero. Here you can find some of my publications on mathematics, which are somehow related to division by zero.

Division by zero can be found in various places in mathematics: the sine theorem, the equation of the straight line y=kx and so on. I suggest you explore these formulas on your own. Write about your results in the comments. If necessary, I will show you under what conditions division by zero appears there.

What is division by zero, I will definitely tell you in the future. But before that, there will be many more interesting things.

Trigonometry value table for engineers

For engineers, a trigonometry table of values should contain numbers so that calculations can be done quickly.

Trigonometry value table for engineers

Division by zero is not as important for engineers as it is for physicists. Mathematicians have learned to bypass problem areas in engineering calculations. But physicists in their theories can meet division by zero much more often. If you already want to know what is the result of division by zero in your theoretical research, write in the comments, I will try to help you.

Mathematical operations with infinite series

Annotation

When performing mathematical operations with infinite series, it is necessary to follow the rules of the positional number system.

Number of terms

The number of terms of an infinite series, presented in the visible part of the series, must be considered as an analogue of writing a number using numbers in the positional number system. The number of terms in the visible part of the series is similar to the rounding of an ordinary decimal fraction with a certain accuracy, that is, to a certain number of decimal places.

When performing mathematical operations with infinite series, for each example it is necessary to use the same number of terms in the visible part of the series. If you do not follow this rule, it can lead to an erroneous result. In mathematics, it is not customary to use any number with different rounding accuracy in one example.

Shifting series

Shifting an infinite series when performing mathematical operations automatically leads to an incorrect result. This is analogous to adding zeros to the decimal immediately after the decimal point.

Consider an example. If you subtract the same series without a shift from any series, the result will be zero. If the subtraction uses a shift and does not take into account the compensating group of terms, then the result will be different from zero. Suppose we have a series S. Let's write the series -S and add these two series. The result should be zero. By performing addition without shift, we get the correct result.

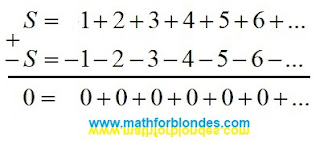Addition of infinite series without shift

Shift by one position leads to wrong result.

Shift by one position

A two-position shift leads to another incorrect result.

A two-position shift

Shifts by an arbitrary number of positions allow you to get an infinite number of incorrect results.

Compliance with the rule about the same number of terms of an infinite series in one example and the use of the compensating group of terms (highlighted in curly brackets) avoids an error. But in the examples given, this method is more laborious than no shift.

The use of a compensating group of terms

You can understand the reason for the occurrence of incorrect results if you consider the shift in arithmetic.

Let us analyze some of the most well-known examples of determining the sums of infinite divergent series.

Sum of Grandi's series

In the given example, the sum of Grandi's series is equal to 1/2, which is not a correct result.

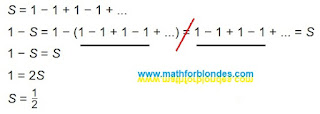Sum of Grandi's series

The second line contains an equals sign between two different sums: one sum consists of five terms that are not equal to zero, the second consists of four. In this example, the optical illusion of the equality of different sums is used, if one term is hidden behind the three-dots of infinity.

The sum of the alternating series

Below is an alternating series and a solution for determining its sum.

The sum of the alternating series

In the proposed solution, the same series is represented by a different number of terms: from four to six. When performing mathematical operations and rearranging terms, the compensating group of terms is ignored. Two other methods for obtaining the sum 4s are not considered: addition of series without shift and multiplication of the original series s by 4. Both these methods give the same result, which indicates the mathematical accuracy of the calculations performed.

The sum 4s

Sum of natural numbers

Consider the sum of an infinite series of natural numbers. Intuitively, this is a divergent infinite series that cannot have a finite sum value. But, here is an example of calculating the sum of this infinite series.

Sum of natural numbers

Typical errors of these calculations are shown in the example above. Mathematicians did not check the solution: the original series c, multiplied by minus three, is equal to:

Solution verification

Conclusion

All the above ways of finding the sum of an infinite series are nothing more than fitting the solution to a given result. Nobody prevents mathematicians from establishing their own rules for virtual games in numbers. But the application of such results of "calculations" in the laws of physics leads to their misunderstanding. For example, a numerical coefficient due to some physical parameter or simply a correction factor is interpreted as the sum of some infinite series. An example of an erroneous interpretation of numerical coefficients would be the following statement: the area of a right triangle is equal to the sum of the Grandi series multiplied by the product of its legs.

More interesting math ideas on the page "My Math"

Permutation of terms in infinite sums

From the school bench, everyone knows the rule that appeared in antiquity: the amount does not change from the rearrangement of the terms. By default, it is assumed that the number of terms and their value remain unchanged. If we change the number of terms or change the value of at least one of them, there can no longer be any talk of rearranging the terms. In this case, we have moved from one sum to another and these two sums are not connected in any way.

In the article “What is wrong with the rearrangement of terms?” (in Russian) an example of an infinite sum is given, allegedly proving that the final sum depends on the order of addition.

Infinite sum

After opening the brackets and reducing the same terms, the result of the addition is different. That's what mathematicians say. Let's consider this example with more careful observance of the rules for writing mathematical expressions.

Permutation of terms in infinite sums

The first line contains the original infinite sum, consisting of six brackets - three terms in each bracket. The total number of terms is 18, the total sum of the expression is zero. The entire mathematical expression can be divided into two groups: the visible part of the expression, represented by 18 terms, and the invisible part of the expression, consisting of an infinite number of brackets, three terms in each bracket. These two parts are separated by the three-dots of infinity. Both parts are zero.

The second line shows the same 18 terms after the permutation. The first three pairs of terms will be further presented in the visible part of the expression. Curly brackets highlight the compensating group of terms.

In the third line, the six terms of the visible part remain unchanged. The compensating group, after simplifying the expression, is represented by three terms. The final result after rearranging the terms has not changed and is still equal to zero.

The fourth line has nothing to do with mathematics. This is the usual trick of an illusionist who hid the compensating group of terms in the arm of infinity (the invisible part of the expression). The purpose of this trick is to convince gullible viewers of the “truthfulness” of the false statement about the change in the total amount after rearranging the terms. Yes, this is what card cheaters do - they hide the card in their sleeve or take it out of there. In the circus, such a trick is called an illusionist's trick. In legal terms, this is called fraud.

We can also give a cruder example of a permutation of the terms in this expression. If terms with only one sign are shown in the visible part of the expression, the audience will inevitably have a question where the terms with opposite signs have gone, and this will clearly make it difficult to demonstrate the trick.

The permutation of terms in infinite sums clearly demonstrates the principle of communicating vessels. The first vessel is the visible part of the expression. The second vessel is the invisible part of the expression, which includes the compensating group of terms. The three-dots of infinity is the connecting pipe between the vessels. The final sum of the expression is the total volume of liquid in the two vessels. Since in our mathematical example the total sum is equal to zero, then in relation to communicating vessels, we consider the initial total liquid level in the vessels as zero of the relative coordinate system. A change in the number or size of terms in the visible part of the expression will lead to a change in the number or size of terms in the compensating group.

If the last expression is considered without an invisible compensating group of terms, then it will not be the result of a rearrangement of the terms, but a completely different infinite sum, containing only a part of the terms from the original expression and not connected with it in any way. The proof of this fact is the different total sum of the two expressions.

More interesting math ideas on the page "My Math"