Trigonometric functions in a rectangle

Published on 7 July, 2016
"The Papers of Independent Authors"
Volume 36 of p. 46-69

Annotation

Representation of trigonometric functions in a rectangle allows to unite algebra, geometry and physics in a single whole.

Short analysis of trigonometric functions

Usually trigonometric functions of plane angle are defined in a rectangular triangle as ratios of the parties of this triangle [a reference to the source in the printing edition].

Trigonometric functions in a triangle

If to accept the definitions of trigonometric functions entered by mathematicians in a rectangular triangle, then values of these functions depend only on a ratio of the sizes of the parties of a triangle. The size of angles in a rectangular triangle is in the range of trigonometrical angles. Trigonometric functions have no signs and do not possess periodic. These properties are homocentrism elements.

The homocentrism mathematics is a mathematics in which the result depends on the option of the relative mathematics accepted by us or on our opinion. Striking examples of a homocentrism in mathematician are: division of numbers on positive and the negative, decimal numeration, numbers and inverse numbers, Cartesian coordinate system, etc.

In Cartesian coordinate system trigonometric functions are defined as coordinates of points of a unit circle [a reference to the source in the printing edition].

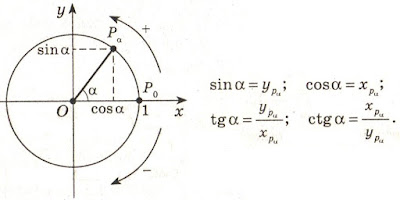Trigonometric functions in Cartesian coordinate system

This definition is possible only because for any point of a circle of coordinate are used as padding elements for creation of a rectangular triangle. For cross points of a circle and coordinate creation of a triangle is impossible.

For any point of the plane in Cartesian coordinate system trigonometric functions can be defined as the relation of coordinates of this point or the relation of coordinates of a point to distance from a point to the center of a frame. An exception is the cross point of coordinate (the center of a frame) for which trigonometric functions cannot be defined. This fact is congenital defect of Cartesian coordinate system. If it is necessary to define trigonometric functions for the point coinciding with the center of a frame, then the frame needs to be displaced aside.

In Cartesian coordinate system trigonometric functions are the relative and depend on the relative positioning of the plane on which the considered points, and frames are located. Periodicity of trigonometric functions is result of rotation of a piece around the center of a frame. Signs of trigonometric functions depend on the positive direction of coordinate accepted by us. All this result homocentrism of views of trigonometric functions.

Signs of trigonometric functions "+" and "-" serve for orientation in space of Cartesian coordinate system. In mathematical formulas with use of trigonometric functions, the sign "minus" at function automatically changes addition for a subtraction or a subtraction on addition. In formulas it is possible to do without the negative values of trigonometric functions. It will allow to reduce twice amount of values of trigonometric functions, but will increase quantity of formulas.

At the following lesson we will consider
Transformations of a triangle to a rectangle

More interesting math ideas on the page "My Math"

Measurement of plane angles

Published on 7 July, 2016
"The Papers of Independent Authors"
Volume 36 of p. 43-45

Annotation

Plane angles need to be divided into trigonometrical angles and rotation angles.

Measurement of angles in a solid geometry

In a solid geometry «angle between a straight line and the plane is called angle between this line and its projection (orthogonal) to the plane. If the straight line to be a perpendicular plane, then angle between it and the plane is considered (my italic type – Nikolaj Khizhnjak) equal 90°, and between a parallel straight line and the plane – equal 0°". [1, p. 308].

As appears from definition, the angle between a straight line and the plane cannot be more than 90°. Angles more than 90° fall into to angles of rotation [2, p. 81]. In a solid geometry it is not accepted to describe by means of angles rotation of a straight line around a point of its crossing with the plane.

If the straight line is parallel to the plane (or belongs to the plane), then it is considered, that the size of the angle has zero value. Actually there is no vertex of angle – a cross point of a straight line and the plane. If the perpendicular plane straight line, then a trace turns into a point which coincides with a cross point of a straight line and the plane. Actually there is no second ray forming a angle. In this case the angle is considered right angle.

Measurement of angles in a planimetrics

On analogies to a solid geometry, a plane angle between two straight lines (line segments) it has to be measured as a angle between a point on one direct and its projection on other straight line with vertex of angle in a cross point of these straight lines.

This rule allows to divide plane angle into trigonometrical angles (from 0° to 90°) and rotation angles. The fundamental difference between these angles consists in amount of the objects on the two dimensional plane forming a angle. The trigonometrical angle is measured between two different objects, the rotation angle is measured between two provisions (initial and terminating) one object. For trigonometrical angles the time factor is absent, for rotation angles the time factor is obligatory: tentative situation, rotation time, terminating situation.

At measurement of angles between two parallel straight lines the angle cannot be defined because there is no cross point of straight lines. At measurement of a corner between two perpendicular straight lines the angle cannot also be defined because the projection of a point coincides with a cross point of these straight lines.

Conclusion: zero and right angles cannot have just the same mathematical properties as other angles. In more detail these distinctions will be described by consideration of trigonometric functions.

Angles and distances

The trigonometrical angle on the properties is similar to distance between two points, the rotation angle is similar to the passable way between the same points. If driving is carried out in a straight line, then the passable path is equal to distance between initial and terminating points of a way. If rotation is carried out on a angle to 90°, then the angle of rotation is equal to a trigonometrical angle. The rotation angle cannot be less trigonometrical angle, the passable path cannot be less than a distance between points of the beginning and end of this way. The distance between two points can be in the numerical range from zero ad infinitum. Compliance between angles from 0° to 90° and numbers from zero ad infinitum is established by a trigonometric function of a tangent of these angles.

The passable path is also expressed in the numerical range from zero ad infinitum even if the distance between an initial and finishing point of the passable way is equal to zero. In the same way the rotation angle can reach infinitely great values, at the same time the trigonometrical angle between the beginning and the end of rotation can be equal to zero. In this case it is possible to establish direct analogy between number and size of a angle as it is accepted in a calculus.

Various mathematical tools, for example, a Pythagorean theorem are used to calculation of distance between initial and terminating points of the passable path. Reduction formulas of angles are applied to definition of a angle between the beginning and the end of rotation.

Conclusion: plane angle on the properties are similar to distances on the plane.

Literature

1. Zabelyshynskaia M.Y."Mathematician. Educational and practical reference book" Kharkiv, Ranock, 2010.
2. Khizhnjak Nikolaj «Bases of mathematics», The Papers of Independent Authors, vol. 19, 2011.

P.S. This article is published for a warming up. Article about trigonometric functions in a rectangle will be a headliner of new work. I hope, from it you learn a lot of new and interesting.