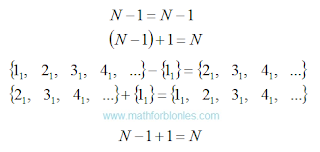Borsch trigonometry. Addition.

I will not tell you recipes for cooking borsch, I will talk about mathematics. What is borsch? These are vegetables cooked in water according to a specific recipe. I will consider two source components (vegetable salad and water) and the final result is borsch. Geometrically, this can be thought of as a rectangle in which one side is a salad, the other side is water. The sum of these two sides is borsch. The diagonal and area of such a rectangle are mathematical concepts and are never used in recipes.

Borsch trigonometry

How do salad and water turn into borsch? How does the sum turn into trigonometry? To understand this, linear angular functions will help us.

The linear angular functions

There are no linear angular functions in mathematics textbooks. But without them there can be no mathematics. Mathematical laws work whether we know them or not.

The linear angular functions are the laws of addition. This is how algebra turns into geometry, and geometry turns into trigonometry.

Trigonometry addition

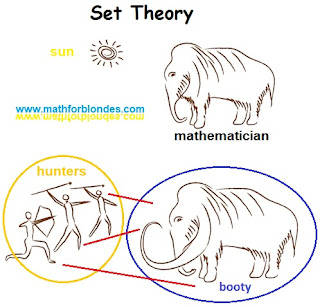
The main law of addition, which mathematicians do not like to talk about, requires that the summands have the same units of measurements. For salad, water and borsch it can be units of weight, volume, value or others.

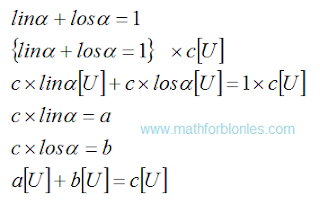Law of addition

The figure shows two levels of difference. The first level is differences in the field of numbers. This is what mathematicians do. The second level is the difference in the area of units of measurement (shown in square brackets). Physicists are doing this. We can understand the third level - the differences in the field of described objects. Different objects can describe the same number of identical units of measurements. How important this is, the trigonometry of borscht will show us. Here is how linear angular functions for borsch will look.

The law of addition for borsch

Part of the water and part of the salad give one serving of borsch. Now we can see what will happen when the angle of linear angular functions changes.

The angle is zero

The angle is zero. We have a salad but no water. You can’t cook borsch. The amount of borsch is also zero. This does not mean that zero borsch is equal to zero water. Zero borsch can be at zero salad (right angle).

The angle is greater than zero, but less than the right angle

The angle is greater than zero, but less than forty-five degrees. We have a lot of salad, but not enough water. The result is a thick borsch.

The angle is forty-five degrees. We have an equal amount of water and lettuce. Perfect borsch (forgive me the cook, it's just math).

The angle is more than forty-five degrees, but less than ninety degrees. We have a lot of water and a little salad. Get liquid borsch.

Right angle

Right angle. We have water. From the salad there were only memories. We cannot cook borscht. The amount of borscht is zero. In this case, drink water.

Something like this. If you're tired of borscht, check out a few other stories.

Percentage.

Percentage

Cell division.

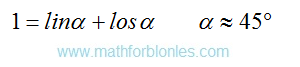Cell division

Two friends had their shares in the general business. After killing one of them, everything went to another.

The general business

The emergence of mathematics on our planet.

The emergence of mathematics

All these stories in the language of mathematics are presented using linear angular functions. I will tell you separately about the real place of these functions in the structure of mathematics. In the meantime, we return to the trigonometry of borscht and consider the projections.

Mathematicians lie

I watched the video One minus one plus one minus one - Numberphile. Mathematicians lie. They did not perform an equality test in the course of their reasoning.

Mathematicians lie

Confirmation of my reasoning about infinite sets.

If you take a closer look at all the manipulations, the error will immediately become visible. The example is written on one line and "equality" is based on the optical illusion of similarity between two different mathematical expressions. Let's write down all actions in a column, starting with the equality 1-S = S.

False equality

As you can see from this example, on opposite sides of the equal sign there are a different number of terms, on the left there is one more term. Equality cannot be fulfilled if this term is not equal to zero. So the given "proof" is a common lie. I have no doubt that other "proofs" of the sum of this infinite series are also based on false statements.

Infinite set

Concluding the discussion of sets, you need to consider an infinite set. The fact is that the concept of "infinity" acts on mathematicians, like a boa constrictor on a rabbit. A trembling horror of infinity deprives mathematicians of common sense. Here is an example:

Infinite set

Alpha denotes a real number. The equal sign in the above expressions indicates that if you add a number or infinity to infinity, nothing will change, the result will be the same infinity. If we take an infinite number of natural numbers as an example, then the considered examples can be represented in the following form:

The set of natural numbers

To illustrate their point, mathematicians have come up with many different methods. Personally, I look at all these methods, as the dances of shamans with tambourines. In fact, they all boil down to the fact that either part of the rooms are not occupied and new guests are accommodated in them, or that some of the visitors are thrown out into the corridor to make room for guests (very humanly). I outlined my view on such decisions here in the form of a fantastic story about the Blonde. What is my reasoning based on? Relocating an infinite number of visitors requires an infinitely long time. After we vacated the first room for the guest, one of the visitors will always walk along the corridor from his room to the next one until the end of the century. Of course, the time factor can be stupidly ignored. It is mathematicians who are trying to manipulate hotel room numbers, convincing us that you can insert something that, in principle, cannot be inserted.

I will demonstrate the logic of my reasoning to you as an example of an infinite number of natural numbers. First you need to answer a very simple question: how many sets of natural numbers exist - one or many? The correct answer to this question does not exist, since we thought up the numbers ourselves; in Nature there are no numbers. Yes, Nature knows how to count, but for this she uses other mathematical tools that are not familiar to us. As Nature believes, I will tell you another time. Since we came up with numbers, we will decide how many sets of natural numbers exist. Consider both options, as befits a real scientist.

Option one. "Let us be given" one single set of natural numbers, which lies serenely on the shelf. We take this set from the shelf. Everything, there are no other natural numbers on the shelf and there is nowhere to take them. We cannot add one to this set, since we already have one. And if you really want to? No problem. We can take a unit from the set already taken by us and return it to the shelf. After that, we can take a unit from the shelf and add it to what we have left. As a result, we again get an infinite number of natural numbers. All our manipulations can be written like this:

One set of natural numbers

I wrote down the actions in the algebraic notation and in the notation adopted in set theory, with a detailed listing of the elements of the set. The subscript indicates that the set of positive integers is one and only. It turns out that the set of natural numbers will remain unchanged only if you subtract unit from it and add the same unit.

Option two. We have on the shelf many different infinite sets of natural numbers. I emphasize - DIFFERENT, despite the fact that they are practically indistinguishable. We take one of these sets. Then we take unit from another set of natural numbers and add to the set we have already taken. We can even add up two sets of natural numbers. Here's what we get:

Many sets of natural numbers

The subscripts “one” and “two” indicate that these elements belonged to different sets. Yes, if you add one to an infinite set, the result will also be an infinite set, but it will not be the same as the original set. If we add another infinite set to one infinite set, the result is a new infinite set consisting of elements of the first two sets.

Set of natural numbers are used for counting in the same way as a ruler for measurements. Now imagine that you added one centimeter to a ruler. This will be a different a ruler, not equal to the original.

You can accept or not accept my reasoning - this is your personal matter. But if you ever run into mathematical problems, think about whether you are following the path of false reasoning, trodden by generations of mathematicians. After all, classes in mathematics, first of all, form a stable stereotype of thinking in us, and only then they add mental abilities to us (or vice versa, deprive us of free thinking).

Set and subset

How to divide a set into subsets? To do this, it is necessary to introduce a new unit of measure that is present in some elements of the selected set. Consider an example.

Suppose we have a set of A, consisting of four people. This set is formed on the basis of "people." We denote the elements of this set by the letter "a", the subscript with a number will indicate the serial number of each person in this set. We introduce a new unit of measurement "gender" and denote it with the letter "b". Since sexual characteristics are common to all people, we multiply each element of the set A by sexual characteristic b. Please note that now our multitude of “people” has turned into a multitude of “people with sexual characteristics”. After that, we can divide the sexual characteristics into male bm and female bw sexual characteristics. Now we can apply the mathematical filter: we choose one of these sexual characteristics, no matter which one - male or female. If it is present in a person, then we multiply it by one; if there is no such sign, we multiply it by zero. And then we use ordinary school math. See what happened.

Set and subset

After multiplication, contractions, and rearrangements, we got two subsets: a subset of Bm men and a subset of Bw women. Mathematicians reason the same way when they apply set theory in practice. But they don’t dedicate us in detail, but give the finished result - "a set of people consist of a subset of men and a subset of women." Naturally, you may wonder how correctly mathematics is applied in the above transformations? I dare to assure you that, in essence, everything was done correctly; it’s enough to know the mathematical justification of arithmetic, Boolean algebra and other branches of mathematics. What it is? Some other time, I'll tell you about it.

You can combine two sets into one by selecting the unit of measure present in the elements of these two sets.

As you can see, units of measure and ordinary mathematics turn set theory into a relic of the past. A sign that the set theory is not all right is that for set theory mathematicians have come up with their own language and their own notation. Mathematicians did what shamans once did. Only shamans know how to "apply" their "knowledge" correctly. They teach us this "knowledge".

In conclusion, I want to show you how mathematicians manipulate infinite sets.

The formation of the set

I have already told you that set theory is a herd theory by which shamans try to sort out "sea urchins" of reality. How do they do that? How does the formation of the set actually occur?

Initially, individual elements stand out from reality. After that, a set are formed from some elements that have a common property. Shamans always know in advance how a set they want to show us.

I will show the process by example. We select "red solid with holes" - these are our elements. At the same time, we see that these elements are with a bow, and there are without a bow. After that, we select some of the elements and form a set of "with a bow." This is how shamans get their food, tying their set theory to reality.

Now let's take a “solid with holes with a bow” and combine these elements by color, selecting red ones. We got a set of red. Now the question is: the resulting sets "with a bow" and "red" - is it the same set or two different sets? Only shamans know the answer.

This simple example shows that set theory is completely useless when it comes to reality. What's the secret? We formed a set of "red solid with holes with a bow". The formation took place in four different units of measurement: color (red), strength (solid), integrity (with holes), jewelry (with a bow). Only a set of units of measurement allows us to adequately describe real objects in the language of mathematics. Here is how it looks.

The formation of the set

The letter "a" with different indices indicates different units of measurement. In brackets, the units of measurement that are considered at the preliminary stage are highlighted. The unit of measure by which the set is formed is the set out of brackets. The last line shows the final result - an element of the set. If we use units of measure to form a set, then the result does not depend on the order of our actions. And this is mathematics, and not the dancing of shamans with tambourines. Shamans can "intuitively" reach the same result, arguing for its "evidence", because units of measurement are not included in their "scientific" arsenal.

Using units of measure, it is very easy to split one set into several subsets, or to combine several sets into one set. Let's take a closer look at the algebra of this process.

Element of the set

If mathematicians cannot reduce the concept of "set" to other concepts, then they do not understand anything in mathematics. I answer the question: how are the elements of one set different from the elements of another set? The answer is very simple: numbers and units of measurements.

Today everything belongs to some kind of set (as mathematicians assure us). By the way, did you look at yourself in the mirror? Have you seen on your forehead a list of those sets to which you belong? And I have not seen such a list. I will say more - not a single thing in reality has a tag with a list of sets to which this thing belongs. Sets are shamans' inventions. How do they do it? Let's recall the history and see how the elements of the set looked like before the mathematician-shamans pulled them into their sets.

Once upon a time, when no one had heard of mathematics, and only trees and Saturn had rings, huge herds of wild elements of sets roamed the physical fields (after all, shamans had not yet invented mathematical fields). They looked something like this.

Sea urhin

Yes, do not be surprised, from the point of view of mathematics, all the elements of sets are most similar to sea urchins - from one point, like needles, units of measurements stick out in all directions. For those who missed something, I remind you that any unit of measure can be represented geometrically as a segment of arbitrary length, and a number as a point. Geometrically, any value can be represented as a bunch of segments sticking out in different directions from one point. This point is point zero. I will not draw this work of geometric art (no inspiration), but you can easily imagine it.

What units of measurements form an element of the set? Any, describing this element from different points of view. These are the ancient units of measurement used by our ancestors and which everyone has long forgotten about. These are the modern units of measurement that we use now. These are units of measurement unknown to us that our descendants will come up with and which they will use to describe reality.

We figured out the geometry - the proposed model of the elements of the set has a clear geometric representation. What about physics? Units of measurement - this is the direct connection of mathematics with physics. If shamans do not recognize units of measurement as a full-fledged element of mathematical theories, this is their problem. Personally, I can’t imagine real math science without units of measurement. That is why, at the very beginning of the story about set theory, I spoke of it as a Stone Age.

But let us pass to the most interesting thing - to the algebra of elements of sets. Algebraically, any element of a set is a collection of different quantities. It looks like this.

Element of the set

I deliberately do not apply the conventions adopted in set theory, since we consider the element of the set in its natural environment before the advent of set theory. Each pair of letters designates a separate quantity consisting of a number indicated by the letter "n" and a unit of measurement indicated by the letter "a". Indexes indicate that the numbers and units are different. One element of the set can consist of an infinite number of quantities (how much imagination we have and our descendants). Each value is geometrically depicted as a separate segment. In the example with the sea urchin, one value is one needle.

How do shamans form sets of different elements? In fact, by units of measurement or by numbers. Without understanding anything in mathematics, they take different sea urchins and carefully examine them in search of the only needle by which they form a multitude. If there is such a needle, then this element belongs to the set, if there is no such needle, it is an element of another set. Shamans tell us tales about thought processes and a single whole.

As you may have guessed, one and the same element can belong to very different sets. Further I will show you how the sets, subsets and other attributes of shamans are formed.

Set and multiset

The concepts of “set” and “multiset” are two trump ace in the sleeves of a sharpie, one in each sleeve. The sharpie takes out from the sleeve that trump ace, which is more convenient for him to get. In any case, the sharpie always wins. In the same way, any mathematician will always justify set theory.

There can’t be two identical elements in a set, but if there are identical elements in a set, such a set is called a “multiset.” Intelligent beings can never understand such a logic of absurdity. This is the level of talking parrots and trained monkeys. Mathematicians act as ordinary animal trainer, preaching to us their absurd ideas.

Once the engineers who built the bridge, during the testing of the bridge, were in a boat under the bridge. If the bridge collapsed, a mediocre engineer died under the rubble of his creation. If the bridge could withstand the load, a talented engineer built other bridges.

No matter how mathematicians hide behind the phrase “mathematics studies abstract concepts”, there is one umbilical cord that inextricably connects them with reality. This umbilical cord is money. We apply the mathematical set theory to the mathematicians themselves.

We studied mathematics very well and now we are giving out salaries. Here comes a mathematician for his money. We count the whole amount to him and lay out on his table on different piles, into which we place banknotes of the same denomination. Then we take one banknote from each pile and hand over to the mathematician his "mathematical set of salary." We explain the mathematics that he will receive the remaining bills only when he proves that a set without the same elements is not equal to a set with the same elements. After that, the most interesting will happen.

Set and multiset

First of all, the logic of the deputies will work: "It can be applied to others, but not to me!" Further, the mathematician will assure us that on banknotes of the same denomination there are different numbers of banknotes, therefore they cannot be considered the same elements of the set. Well, we count the salary in coins - there are no numbers on the coins. Here, the mathematician will frantically recall physics: different coins have different amounts of dirt, the crystal structure and arrangement of atoms of each coin is unique ...

And now I have the most interesting question: where is the line behind which the elements of the multiset turn into the elements of the set and vice versa? Such a facet does not exist - shamans decide everything, science is absent here.

You see that the same set of elements is both a multitude and a multiset at the same time. How right? And here the mathematician-shaman-schuller takes an ace from his sleeve and begins to tell us either about the multitude or the multiset. In any case, he will convince us that the theory of sets is correct.

To understand how modern shamans apply set theory to reality, it is enough to answer one question: how do the elements of one set differ from the elements of another set? I will show you how to do it.

Set theory

Set Theory

Set theory is the stone age of mathematics. Only shamans know how to properly form the set. Let's look at set theory from the side and reveal some of the secrets of shamans. To understand the essence of set theory, it is necessary to consider another mathematical concept - a function. The function sets the correspondence between the elements of two sets. Each element from the herd of hunters is associated with one or more elements from the herd of prey, each element from the herd of prey is assigned one or more elements from the herd of hunters. Only shamans know what kind of herd belongs to and how to divide prey properly.

What is set theory? This is a herd theory. What will happen if we combine a herd (set) mathematicians and a herd (set) sheep: sheeps with a mathematical education or mathematicians with sheep’s brains? I don’t know what set theory says about the results of such a union, but in reality mathematicians will have a great barbecue picnic. I have nothing against set theory, as one of the mathematical tools. But to stand up for “scientific” theories based on such a primitive and vague concept is already too much.

Any theory should be tested by practice, even mathematical. I will show you an example of the practical application of set theory by the example of such concepts as “set” and “multiset”.

More interesting math ideas on the page "My Math"

Achilles and the tortoise

Achilles and the tortoise

In the fifth century BC, the ancient Greek philosopher Zeno of Elea formulated his famous aporia, the most famous of which is the Achilles and the Tortoise aporia. Here’s how it sounds:

Suppose Achilles runs ten times faster than a turtle, and is a thousand paces behind it. During the time that Achilles has run this distance, the tortoise will crawl a hundred steps in the same direction. When Achilles runs a hundred paces, the tortoise crawls ten more steps, and so on. The process will continue indefinitely, Achilles will never catch up with the tortoise.

Another version of the aporia "Achilles and the tortoise":

In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.

This reasoning was a logical shock for all subsequent generations. Aristotle, Diogenes, Kant, Hegel, Hilbert ... All of them in one way or another viewed the aporia of Zeno. The shock turned out to be so strong that discussions are continuing at the present time; the scientific community has not yet succeeded in reaching a general opinion on the essence of paradoxes. Mathematical analysis, set theory, new physical and philosophical approaches were involved in the study of the question; none of them has become a generally accepted solution. Everyone understands that this is a hoax, but no one understands what it is.

From the point of view of mathematics, Zeno in his aporia clearly demonstrated the transition from quantity to an inverse quantity. This transition implies the use of variable units of measurement instead of constants. As far as I understand, the mathematical apparatus for using variable units of measurement has either not yet been developed or has not been applied to the aporia of Zeno. The application of our usual logic leads us into a trap. We, by the inertia of thinking, apply constant units of time to the reciprocal. From a physical point of view, it looks like a slowing down of time to its full stop at the moment when Achilles approaches the turtle. If time stops, Achilles can no longer overtake the turtle.

If we turn the logic we are used to, everything falls into place. Achilles runs at a constant speed. Each subsequent segment of its path is ten times shorter than the previous one. Accordingly, the time spent on its overcoming is ten times less than the previous one. If you use the concept of "infinity" in this situation, then it will be correct to say "Achilles will catch up to the tortoise infinitely quickly".

How to avoid this logical trap? Stay in constant time units and don’t go to inverse quantity. In the language of Zeno, it looks like this:

In the time that Achilles has run a thousand steps, the tortoise will crawl a hundred steps in the same direction. Over the next interval of time equal to the first, Achilles will run a thousand more steps, and the turtle will crawl a hundred steps. Now Achilles is eight hundred paces ahead of the tortoise.

This approach adequately describes reality without any logical paradoxes. But this is not a complete solution. On the aporia of Zeno "Achilles and the Turtle" is very similar to Einstein's statement about the irresistible speed of light. We still have to study, rethink and solve this problem. And the solution must be sought not in infinitely large numbers, but in units of measurement.

Another interesting aporia of Zeno tells of a flying arrow:

A flying arrow is motionless, because at each moment of time it is motionless, and since it is motionless at each moment of time, it is always motionless.

In this aporia, the logical paradox is overcome very simply - it is enough to clarify that at each moment in time a flying arrow is stationary at different points in space, which, in fact, is movement.