Quantity

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
The infinite trigonometric functions

Lesson 6

Quantity

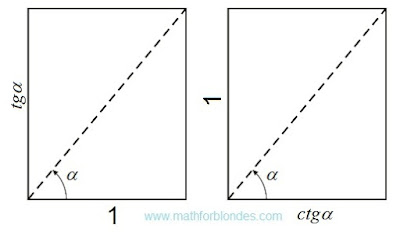Tangent and cotangent

Mathematical interpretation of the drawing given above will look as follows.

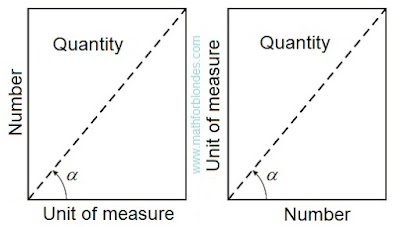Quantity

Both options of representation of quantity are absolutely equal and yield identical result. On a numerical axis the parity of numbers and units of measure looks so.

Numbers on a straight line

In this case zero and unit divided into zero act as the horizons which cannot be reached by means of numbers. For further transformation of quantity to a look habitual to us, to the abstract mathematical concepts it is necessary to enter homocentrism elements.

If we consider that across units of measure settle down, and numbers are perpendicular them, then quantity will have two options of representation.

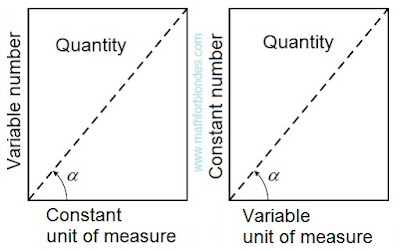Two options of quantity

The numerical axis takes the following form.

Numerical axis with units of measure

Introduction of the following element of a homocentrism allows to pass to habitual representation of quantity. If we consider that the unit of measure always remains to a constant, then for the adequate description of quantity it is necessary to enter inverse numbers. The inverse symmetry of numbers is result of transition from variable units of measure to constants.

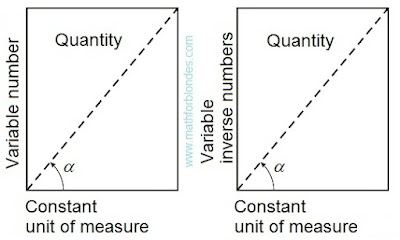Quantity in constant units of measure

The numerical axis will be transformed as follows.

Numbers and inverse numbers

In this case the numerical axis is represented without imposing of a reflecting symmetry. Unit acts as a point of the inverse symmetry. By the inverse symmetry numbers and units of measure in any quantity are connected. At invariable quantity, decrease of number leads to increase in a unit of measure, increase in number – to decrease of a unit of measure. The algebra of similitudes looks so.

Decrease of number Increase in number

Here elements, the falling into number domains, are represented in round brackets. Elements, the falling into areas of units of measure, are represented in square brackets.

At the following lesson we will consider
Variable units of measure