
It is another icon for hanging out on a wall and overlearnings of text. We this we will not engage in. We will look better, as possible to combine a rectangular triangle and circumference. For this purpose we will combine two pictures: circumference from classic determination of trigonometric functions and our triangle. We will place a triangle next to a circumference. That is it looks.
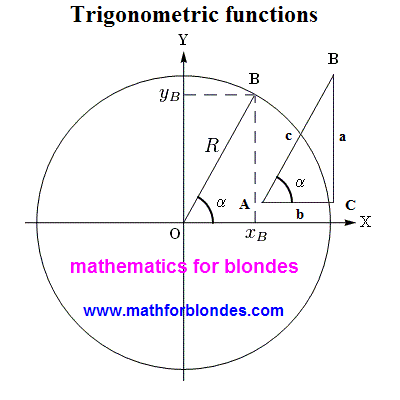
As see, pictures are practically identical, and component elements are named differently in them. Identically mark only corner alpha and point of "B". Now we will impose a triangle straight on a circumference. All graphic images accepted for a circumference we will save, and a rectangular triangle we will underline red lines on the inside (type we will lead around the contour of triangle lipstick).
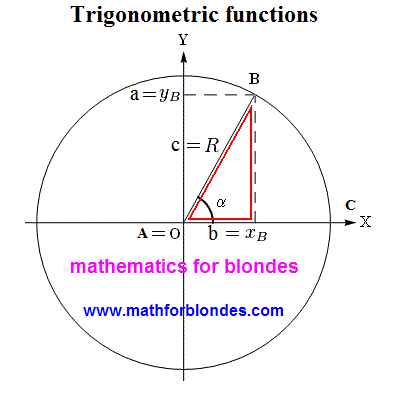
As be obvious from a picture, the hypotenuse of rectangular triangle grows into the radius of circumference, cathetuses become equal to the coordinates of point. It as in a human language - a the same concept in different languages is designated by different words. This distinction in a pronunciation does not give to us to understand foreign languages. Approximately the same takes place in mathematics. Some consider determination of trigonometric functions on a rectangular triangle primitive. If you want to understand mathematics, will memorize the following: there are not primitive things in mathematics. There are primitive creatures counting itself very clever. Exactly desire to seem more clever than other, resulted in that mathematicians almost nothing is understood in mathematics.
Specially I will quote a phrase from Russian-language Wikipedia, where talked about determination of trigonometric functions on a triangle: "This determination has some pedagogical advantage, because does not require introductions of concept of the system of coordinates, but also such large defect, that it is impossible to define trigonometric functions even for obtuse angles that must be known at the decision of elementary tasks about amblygons". Honestly speaking, like thick ignorance of mathematicians simply shocks me. What triangle are trigonometric functions determined for? Correctly, for RECTANGULAR. Let though one mathematician will show to me RECTANGULAR TRIANGLE With OBTUSE ANGLE. I swear to you, as soon as I will see this geometrical miracle, I here will invert the portrait of tangent heels over head and I will hang oneself on a cosine. Not a single mathematician understands really, that the decision of "elementary tasks about amblygons" through trigonometric functions is ALWAYS taken to breaking up of one amblygon on two rectangular triangles?
Now I will show the most primitive example of existence of trigonometry you in life. More primitive, probably, is not already.

Look at a photo - how many human bodies serenely stationed oneself on the horizontal plane of rock, at the same time there is nobody on a vertical plane. Why? And because trigonometric functions for perpendicular direction have quite another values. For us with you basic sense of trigonometric functions is that exactly trigonometric functions determine our possibilities.















No comments:
Post a Comment