In an order to name a next natural number, what number is necessary to be added to the natural number?

In an order to name a next natural number, to the present natural number it is necessary to add 1 (one, unit). Every subsequent natural number anymore than previous on unit. We will consider a few mathematical examples of decision of this task.

Example 1. Let we have a natural number 3 (three). What next natural number? For the receipt of answer we will add to the number 3 (three) a number 1 (one).

3 + 1 = 4

Answer: by a natural number, following by a natural number 3 (three) there will be a number 4 (four).

Example 2. a natural number is Given 16 (sixteen). What natural number following? We add to the number 16 (three) a number 1 (one) and we will get a right answer.

16 + 1 = 17

Answer: natural number 17 (seventeen) will be following by a natural number 16 (sixteen).

Example 3. What natural number does stand after a number 18 592 (eighteen thousands five hundred ninety two) in the natural row of numbers? To the number 18 592 (eighteen thousands five hundred ninety two) we add a number 1 (one) and we get a next number from the row of natural numbers.

18 592 + 1 = 18 593

Answer: number 18 593 (eighteen thousands five hundred ninety three) costs following by a number 18 592 (eighteen thousands five hundred ninety two) in the natural row of numbers.

A general formula for being of next natural number looks so (a plus one is evened b):

a + 1 = b

where а - is the set natural number
         b - next natural number

To check up the got result for the first 120 (one hundred twenty) natural numbers it is possible on the table of natural numbers.

Integers determination

Oddly enough, looked over three different reference books on mathematics - all of them bashfully hold back determination of integers. There was determination of great number of integers in Wikipedia. Specially I will quote this masterpiece of simplicity : the great "number of integers is determined as shorting of great number of natural numbers of relatively arithmetic operations of addition and deduction". Does remain only to ask authors, how many years it will have to the aliens to sit in our academies, they will understand before, what we name integers?

By analogy with determination of natural numbers, we will formulate determination of integers from Nikolay Khyzhnjak: all numbers which can be got as a result of addition of positive and negative units are named integers.

We will consider examples. Number 2 (two) is an integer, as it can be got addition of two units:

1 + 1 = 2

Number -2 (minus two) is an integer, because he can be got by addition of two negative units:

(-1) + (-1) = -2

From the determination formulated by me quite logically do we get an answer for a question: "is there a zero by an integer?". Yes, a zero is this integer which can be got addition of positive and negative unit:

1 + (-1) = 0

A zero is not a positive or negative number.

Natural numbers definition

Determinations of natural numbers, which over are brought in Wikipedia and mathematical literature, contain whatever, except mathematics. If we decided to divide numbers with that it was simpler to rule above them, then competent determination of natural numbers will not prevent to enter mathematically.

Natural numbers definition from Nikolay Khyzhnjak: unit and all numbers which can be got as a result of addition of units are named natural numbers.

For those, who considers that a zero belongs to the natural numbers, this determination will sound so: zero, unit and all numbers which can be got as a result of addition of units, is named natural numbers.

What did we do? We account sticks in a hand replaced units in mathematics. Now we will check in practice, as it works. We will consider a number 2 (two):

1 + 1 = 2

Number 2 is a natural number, because it can be presented as a sum of two units, that corresponds to two account sticks or two other objects "for an account in natural way" (quotation from classic determination of natural numbers).

We will take more difficult example. If broken number 7,5 to divide into other broken number 2,5, will there be a result by a natural number?

7,5 : 2,5 = 3

Yes, as a result of division of two broken numbers we got a natural number 3, as it can be got as a result of addition of three units.

1 + 1 + 1 = 3

If a number scatters on units without noise and dust, such number is natural. For example, number 2,5 (two with a half) is not natural, because except two units with a frightful crash fractional part of number of 0,5 is pushed aside:

1 + 1 + 0,5 = 2,5

Another example. Number -4 (minus four) is not natural, as at decomposition on units a sign falls off minus and lifts the whole heap of dust. Negative numbers it is impossible to get addition of positive units. By the way, in the dust of negative numbers of mathematics roamed, as hedgehogs are in fog. Instead of that to understand reasons of dustborne storm, they thought of the module of number, than yet more all tangled.

I hope, my determination will help you it is better to be oriented in such different names of such identical numbers.

Does a broken number can to be natural? - no, broken numbers do not behave to the natural numbers.

Natural numbers are determination

Determination of natural numbers from Wikipedia: natural numbers are numbers which arise up in natural way at an account. And farther already fuss went with different approaches at by determinations of natural numbers. I have the special page with the generally accepted look to the natural numbers.

I can give another determination of natural numbers: natural numbers are numbers, used for the account of objects or for pointing of sequence number of one or another object among homogeneous objects.

In order to avoid problems in the process of studies, urgently I recommend to learn that determination of natural numbers, which is given in your textbook. In case of necessity, will pronounce him, as quotation from Mathematical Scripture. Looking at natural numbers is possible in the table of natural numbers. If want though something independent to consider, I recommend to read my determination of natural numbers.

Now a bit about history of natural numbers. It appeared in mathematics in those ancient times, when all blondes were natural. As follows from determination of natural numbers, natural numbers are those numbers which it is possible to count blondes. Exactly in honour the natural blondes of mathematics named numbers "natural". If it is possible to count blondes some number - this number natural means, if to count blondes it is impossible - a number means is not natural.

Mathematics for blondes

For example. Shot the one second is not a natural number. Where did you see half-blondes? Or one and a half blondes? All broken numbers are not natural numbers. Negative numbers similarly do not behave to the natural numbers. It is possible to count negative numbers, how many blondes do not seize to every concrete mathematician, but these blondes will be not natural, and virtual. What numbers are natural? Positive integers are natural.

Now interesting question: is a zero a natural number? In the different sacred books of mathematicians there are different opinions on that score. One add a zero on the face of sacred natural numbers, other refuse to the zero in such honour. Most correct decision of this problem - read, that it is written in a textbook or straight will ask the teacher. It is necessary to acknowledge that with a question adding of zero on natural numbers little disorder is created in mathematics. And this little disorder sometimes grows into large mathematical chaos, when business comes to the zero. Division by zero - one of examples.

Table of natural numbers

Table of natural numbers from 1 (one) to 200 (two hundred) is a sequence of positive integers which in mathematics it is accepted to name natural numbers. Here you can get the table of natural numbers free of charge. In a table the natural row of numbers is presented from 1 (units) to 200 (two hundred).

Attention! Zero is a natural number! In Russian mathematics a zero is not a natural number.

Table of natural numbers

The sequence of natural numbers, formative the natural row of numbers is evidently presented in a table. Can this table bravely be named Periodic System of Natural Numbers from Nikolay khyzhnjak))) Why is my row of natural numbers closed on a number 120? Simply to me, as to any respecting itself cat, it was to write laziness farther. If you need the table of natural numbers of largenesses (well, there, to cover a settee) vitally, write in the comments ordering from sizes - I will execute certainly. To the first pussy-cat - free of charge)))

The table of natural numbers will help you masterly to determine the amount of different numbers in natural numbers and satisfy other mathematical needs. The table of natural numbers is worked out in the secret laboratories of extraterrestrial civilizations specially for blondes, in case of cruel interrogations inquisitors from mathematics))) are Presently examine the question of creation of table of natural numbers for a flush-off on mobile telephones (such to itself mathematical body armour).

To get the table of figure (numerals) from 1 to 20 - the table of natural numbers is here presented only, but not figure (numerals). Figure (numerals) exists only ten.

Natural figure (numerals) - numerals are Arabic, Roman et al, and natural are numbers.

Figure (numerals) 100 - one hundred is a number and this number 100 consists of three figure (numerals) is one unit 1 and two zeros 0 and 0. All together these three figure (numerals) form a number 100 - one hundred.

Draw a table of values for the first 6 natural numbers.

Table of primes 2 to 20,000.

Trigonometric table

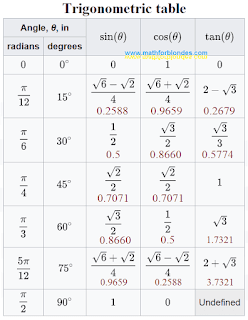
A trigonometric table is a table of values of trigonometric functions. This trigonometric table contains corners in degrees and radians, that very comfortably for translation of degrees in radians and vice versa, radians in degrees. The table of trigonometric values of functions is made with roots square and by shots, that allows to abbreviate shots at the decision of school examples. The sine of sin, cosine of cos, tangent of tg, cotangent of ctg, secant of sec, cosecant of cosec, is presented in a table.

Table of values of trigonometric functions

To facilitate life of blondes, we yet not once will take apart this trigonometric table on the lines of sines, cosines, tangents, cotangents, secants and cosecants, on the columns of degrees and radian, on the separate squares of values of trigonometric functions.

In a trigonometric table presented sine of corner of sin 0, 30, 45, 60, 90, 180, 270 and 360 degrees or 0, pi/6, pi/4, pi/3, pi/2, pi, 3pi/2, 2pi radian. Values of sine of corner of sin 0, 1/2, a root from 2 is divided by 2, a root from 3 is divided by 2, unit and minus unit. A line opposite the letters of sin is named yet table of sines.

The table of values of trigonometric functions contains the cosine of corner of cos 0, 30, 45, 60, 90, 180, 270, 360 degrees. If to transfer these corners in radians, we will get 0 pi, pi/6, pi/4, pi/3, pi/2, pi, 3pi/2, 2pi radian. A table of cosines of these corners is a line opposite the letters of cos, in which unit, root, is writtenin from three divided by two, a root from two is divided by two, one second, zero and minus unit.

First two lines of this table of sin and cos is the table of sines and cosines.

The table of tangents was hidden below than table of sines and cosines in a line with two letters of tg. Oddly enough, but the same are here present tangent of corner of tg 0, 30, 45, 60, 90, 180, 270, 360 degrees. And in radians they are transferred just 0 pi, pi / 6, pi / 4, pi / 3, pi / 2, pi, 3 pi / 2, 2 pi radian. The values of tangents of these corners make a zero, unit is divided by a root from three, unit, root from three and hyphen which is sometimes replaced by the sign of endlessness. It means that mathematicians can not define the value of trigonometric function tangent for corners 90 and 270 degrees. So, blondes, not despair, even mathematicians can not all!

Yet below there is a table of cotangents. We will repeat once again those corners for which the cotangent of ctg is writtenin in a trigonometric table : 0, 30, 45, 60, 90, 180, 270, 360 degrees. And once again we will be trained to transfer degrees in radians: 0 pi, pi/ 6, pi/ 4, pi/ 3, pi/ 2, pi, 3pi/ 2, 2pi radian. The cotangent of corner of ctg begins from a vagueness, marked a hyphen, along go root from three, unit, unit is divided by a root from three, zero.

Two middle lines of trigonometric table are folded in the table of tangents and cotangents.

Two last lines of trigonometric table occupy a secant which is designated sec, and cosecant which is designated cosec. As these trigonometric functions are reverse to the cosine and sine, the values of these functions are reverse to the values of cosine and sine. I turn your special attention on that mathematicians once again made an effort tangle blondes, violating logic of application of prefix of Co. It turned out for them, that a secant is a trigonometric function, reverse to Cosine, and Cosecant, csc - reverse to the sine. Naturally, that for a secant and cosecant there are corners, the values of functions for which are not certain.

Trigonometric  table

Large trigonometric table with fractions and square roots.

Trigonometric table 0 - 90 degrees

You might be interested in:

Trigonometric circle sine cosine
Trigonometric table of sines and cosines
Trigonometric table tangent cotangent in degrees
Trigonometric table in radians
Why is the sine of 30 degrees equal to half one?
Legend about Sine and Cosine

How to find a value:

Table of values of the trigonometric functions
cosecent trigonometric tablestable 4pi/3-2pi
table of trigonometric functions 30 to 360 degrees for students
radians degrees sine cosine tangent chart
six trigonometric functions
mathematics sin cos value table - WAW! it can be seen here!

cos from 0 to pi
table of 6 trig functions 0 to 360
sin 90
sin cos 0 30 45 90 180
trig table pi over
seperate sin cos
table tangent radians pi - you can find on this page.

Trigonometric function of basic corners table - the most widespread in textbooks and examples corners over are brought in a trigonometric table.

Table cosine sine tangent and cotangent free of charge - all these functions are here collected in one table and looking at them is possible quite free of charge.

Trigonometric table of sin cos tan cot - and yet here is sec and csc, in degrees and radians.

Tangent of pi on 4 - how mathematicians are not perverted only, to mask usual unit.

Sine 180 degrees equal - and so mathematicians can mask an usual zero. Straight not mathematics, and woman bag some - while anything will find in her...

sin zero - well here, another zero they hid, true not very much far, but insidiously - in cos 0 after a zero unit is hidden. Try to be not here tangled.

A table of sines and cosines is in radians - well, here the not greatest table, but some radians are present. It will be needed to create anything monumental.

Table of often meeting values of sine of cosine of tangent of cotangent - here are necessary to you values. If you consider that other values meet more often, will report to me about it, I will correct the annoying misunderstanding.

cot 225 degrees - minus is equal to unit (- 1). In a table for the botanists of it it is not, had to hit upon. Bad trigonometric table, it is needed to draw other, specially for series "Trigonometry for blondes".

A table of sines and cosines is in fraction - yes, exactly as a fraction the values of six trigonometric functions are writtenin for some corners in a table on a picture.

School table of tangent - I am here and tangent as a shot, specially for schoolchildren.

To calculate cosecant - here are cosecants in a table.

Table of tangents with the use of pi - after absence the best, while I can offer this table only.

sin cos tg column row - yes, here in a trig table there are both rows and columns.

Value of 30 degree sin table fraction - yes, yes, yes it here.

cosine, tabel trigonometric, tabelul trigonometric - welcome on this page.