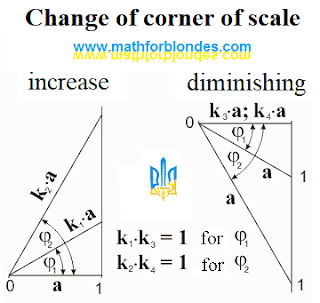
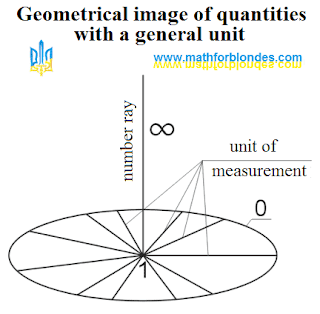
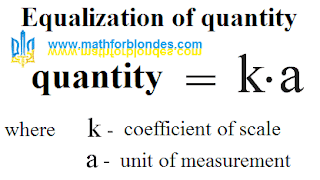Trigonometric circle - comments 2. This continuation of publication of comments to the page the "
Trigonometric circle", left by visitors in the
Russian version of blog "Mathematics For Blondes".
Comment - I am very thankful you, I skipped these themes and there is nothing could understand, and now though that I understand)))
Comment - I in general understood nothing)
Nikolay Khyzhnjak - Nothing, it is not needed to be disordered. All do not can everything it is identically good to understand. A trigonometric circle someone understands well, someone can not understand in general.
Comment - Class site))))))
Nikolay Khyzhnjak - Concerning a site not quite true: here almost is not that it must be are mathematicians. Simple, clear, evident. I will try to reform)))
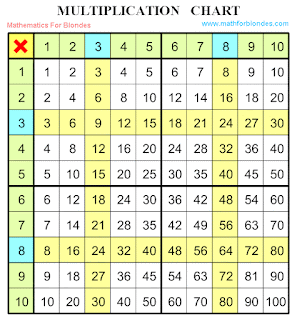
Comment - Your table very pleased me all is simple, evidently and clear. Thank you!!!
Nikolay Khyzhnjak - It is my little strokes to stranger work. The trigonometric circle I will draw together with you straight in this blog. I hope, soon this we will take up)))
Comment - I thank you. I do not present although, how all of it I will teach... But for a crib it very well))
Nikolay Khyzhnjak - And really do the salespeople of estimations require cramming yet?))) Personally I prefer to understand mathematics, but not to learn by rote ridiculous rules)))
Comment - cos pi/12 as possible to present?
Nikolay Khyzhnjak - cos pi/12 = cos (180/12) degrees = cos 15 degrees = 0,9659 Finding this value is possible on the table of cosines.
Comment - cos corner in intervals from pi to 3pi/2 does take on negative values??
Nikolay Khyzhnjak - Yes, in the third fourth at a cosine negative values, as well as in fourth, from 3pi/2 to 2pi.
Comment - how to find the cosine of pi on 12
Nikolay Khyzhnjak - It is hardly higher written in comments, that on the table of cosines it is needed to find a cosine 15 degrees.
Comment - you are dimwits
Comment - Thank you for the name "Mathematics for blondes". I 30 years engage in that I translate school mathematics into the language of "mathematics for blondes". Actuality grew with introduction of single state examination. I add to the line of tangents and cotangents (students understand it).
Nikolay Khyzhnjak - Accept my sincere condolences))) Unlike you, I have a right to be quiet. As a teacher of mathematics, you such right do not have. you are under an obligation to explain ALL themes, I can simply not talk about separate moments.
Yes, lines of tangents and cotangents simply are under an obligation to be on a trigonometric circle. Although I and lazy, but I will try in the near time to draw such picture.
Very interesting me, how do you explain negative and complex numbers in language of blondes?
Comment - creator, for you alike at with a head badly, if you consider blondes fools.
Nikolay Khyzhnjak - I think that my articles "
Mathematics - the blonde searches x", "http://www.mathforblondes.com/2010/11/wunderkindes-and-cretin-with-blondes.html" testify to reverse.
Comment - thank you that who did everything I am a not blonde and not girl but all is even
Nikolay Khyzhnjak - I write for all, who wants to read it)))
Comment - good site, to the author respect and respect, though I and not blonde, I badly understand in mathematics, but all is normally written with a clear language, thank you.
Nikolay Khyzhnjak - Thank you for a comment. Not everybody can understand mathematics - it firstly. Secondly, someone must and mathematicians to feed, dress, write their portraits...
Comment - seems, you similarly are blond.
Nikolay Khyzhnjak - When I became a mathematician, I, seems, began to understand logic of thinking of blondes. Paradox, but for blondes, alike, mathematical character of thinking.