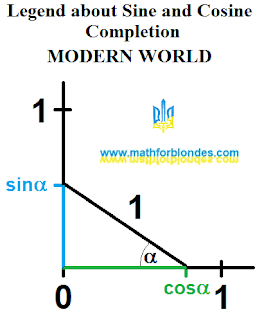
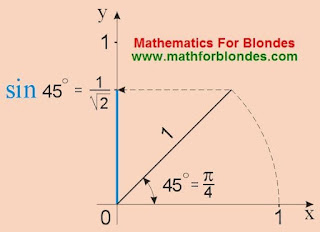
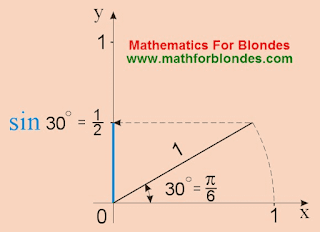
0 = 1
Looks beautifully. But there is a little problem in legitimacy of existence of similar equality - it we. Did you hear the fable of Ivan Krylov "Marmoset and glasses"?
 |
| Ivan Krylov. Marmoset and glasses. |
5 = 5 - undeniable equality, all marmosets approve amicably;
5 = 5 + 0 - was there obvious curiosity on the snouts of marmosets - now there will be something interesting, otherwise why to add a zero to the number?;
Presentiment of marmosets did not deceive - we use equality a "zero is equal to unit" and we put instead of zero unit:
5 = 5 + 1 - marmosets titter;
5 = 6 - marmosets amicably laugh at us, we in bewilderment.
"Any number is equal to any number" is the most terrible nightmare of mathematicians, which we so easily and simply got. Superstitious horror before similar equality is very well described in the story of Ted Chiang "Divizion by Zero". In this fantastic story woman-mathematician managed mathematical methods to divide a number into a zero. She got equality:
any number = any number
Finale of story "Divizion by Zero" tragic enough. But, here is a very interesting question: "Are there glasses by a that universal object which ideally goes Near ALL parts of body of marmoset?". We are not marmosets. We know a right answer - glasses are put exceptionally on a nose for the improvement of sight.
I would not begin to write about equality a "zero equal to unit", if this was the fruit of leisure fiction. But, strangely enough, it is the future of mathematics. That in what we today refuse to believe, tomorrow will be one of basic equalizations of mathematics. True, mathematics then will be other, not for monkeys with glasses.
Here little fact in support of my words. One of leading physicists-theorists, Andrei Linde, in the lecture "Many-sided Universe" said: "The sum of energy of matter and gravity energy in the scales of Universe is equal to a zero".
A zero can be equal to something, different from a zero! you will turn the special attention, that the question in this equality is about SUM, but not difference of two physical sizes. If physicists subtracted from one physical size other is be much simpler. As early as school we taught that if from something to subtract such is exact something, then as a result we will get a zero. But, physicists assure that we need to something to add something and as a result we will get a zero! The law of maintenance of energies in the scale of Universe equals a zero. Our equality a "zero is equal to unit" presents this law in a general view for any pieces, taken in the scales of universe. Strange, it turns out, what the amount of blondes in the scales of Universe must be equal to the zero... And it yet needs to be proved! Where do they, at that rate, go?!
Think, now to our marmosets not to the laughter. Does "this law of maintenance spread to all marmoset or only on her part? If on part, then on which one? If on all marmoset, then does this law operate on other marmosets? If does operate, then on all marmosets without an exception or only on select? If only on select, then who, at that rate, them does elect there? Write down and me!!! I want to be select!")))
As see, every new step in science generates mass of new questions. And for that, what not to look a marmoset with glasses, something needs to be understood. Though slightly.