Trigonometric circle - comments 2. This continuation of publication of comments to the page the "Trigonometric circle", left by visitors in the Russian version of blog "Mathematics For Blondes".
Comment - I am very thankful you, I skipped these themes and there is nothing could understand, and now though that I understand)))
Comment - I in general understood nothing)
Nikolay Khyzhnjak - Nothing, it is not needed to be disordered. All do not can everything it is identically good to understand. A trigonometric circle someone understands well, someone can not understand in general.
Comment - Class site))))))
Nikolay Khyzhnjak - Concerning a site not quite true: here almost is not that it must be are mathematicians. Simple, clear, evident. I will try to reform)))
Comment - Your table very pleased me all is simple, evidently and clear. Thank you!!!
Nikolay Khyzhnjak - It is my little strokes to stranger work. The trigonometric circle I will draw together with you straight in this blog. I hope, soon this we will take up)))
Comment - I thank you. I do not present although, how all of it I will teach... But for a crib it very well))
Nikolay Khyzhnjak - And really do the salespeople of estimations require cramming yet?))) Personally I prefer to understand mathematics, but not to learn by rote ridiculous rules)))
Comment - cos pi/12 as possible to present?
Nikolay Khyzhnjak - cos pi/12 = cos (180/12) degrees = cos 15 degrees = 0,9659 Finding this value is possible on the table of cosines.
Comment - cos corner in intervals from pi to 3pi/2 does take on negative values??
Nikolay Khyzhnjak - Yes, in the third fourth at a cosine negative values, as well as in fourth, from 3pi/2 to 2pi.
Comment - how to find the cosine of pi on 12
Nikolay Khyzhnjak - It is hardly higher written in comments, that on the table of cosines it is needed to find a cosine 15 degrees.
Comment - you are dimwits
Comment - Thank you for the name "Mathematics for blondes". I 30 years engage in that I translate school mathematics into the language of "mathematics for blondes". Actuality grew with introduction of single state examination. I add to the line of tangents and cotangents (students understand it).
Nikolay Khyzhnjak - Accept my sincere condolences))) Unlike you, I have a right to be quiet. As a teacher of mathematics, you such right do not have. you are under an obligation to explain ALL themes, I can simply not talk about separate moments.
Yes, lines of tangents and cotangents simply are under an obligation to be on a trigonometric circle. Although I and lazy, but I will try in the near time to draw such picture.
Very interesting me, how do you explain negative and complex numbers in language of blondes?
Comment - creator, for you alike at with a head badly, if you consider blondes fools.
Nikolay Khyzhnjak - I think that my articles "Mathematics - the blonde searches x", "http://www.mathforblondes.com/2010/11/wunderkindes-and-cretin-with-blondes.html" testify to reverse.
Comment - thank you that who did everything I am a not blonde and not girl but all is even
Nikolay Khyzhnjak - I write for all, who wants to read it)))
Comment - good site, to the author respect and respect, though I and not blonde, I badly understand in mathematics, but all is normally written with a clear language, thank you.
Nikolay Khyzhnjak - Thank you for a comment. Not everybody can understand mathematics - it firstly. Secondly, someone must and mathematicians to feed, dress, write their portraits...
Comment - seems, you similarly are blond.
Nikolay Khyzhnjak - When I became a mathematician, I, seems, began to understand logic of thinking of blondes. Paradox, but for blondes, alike, mathematical character of thinking.
Friday, February 18, 2011
Trigonometric circle - comments

The Russian specialists of Photoshop compelled Paris Hilton to read a book "Discrete mathematics".
Comment - and to me reached!)
Nikolay Khyzhnjak - it is stranger work, this picture of trigonometric circle I only adorned))) it will be Needed to draw the trigonometric circle, by sight clear at first blush)))
Comment - you are a fool bald, explain normally! I am a hard blonde, I understand nothing!
Nikolay Khyzhnjak - If you are a hard fool, then medicine is here powerless. Mathematics - moreover. Now try once again, only already politely, to answer a question: that you are not clear exactly?
Comment - what if at being of value alpha equal 4pi, for me 720 degrees, how farther to find a sine and cosine alpha??
Comment - however I hate geometry, though I am a not blonde=)
Nikolay Khyzhnjak - concerning a hatred. It is your problems((( to Mathematics on a drum, blonde you or no, you love geometry or hate, in mathematics twice two however will equal four, and the laws of geometry will continue to work, as well as before. It is needed simply to reconcile oneself to with this fact. All people can not identically masterly own geometry. But it is desirable to know about basic concepts. In fact you are a reasonable creature, but not animal. It not needed the animal of knowledge, for life by him there are fully enough instincts.
Concerning 720 degrees now I will write on a separate page.
Comment - on my you engage in unavailing enough business. To teach blondes, it too same, that to try to drive away a tram... Although, good luck)
Comment - better will explain on an example - how to decide cos(x - pi/2)
Nikolay Khyzhnjak - Concerning educating of blondes. Blondes are a simply advertising trick))) Although in some places I understand their logic perfectly)))
In business-literature a phrase pleased me: "If not able to do business, teach other people, as needed to do business. If not able to teach people to business, teach teachers, as needed to teach people to business"))) As I in trigonometry small that I understand, I teach other and study. Blondes - it my level just)))
About the decision of examples. Examples without решебника I I am not able to decide. I am simpler to set about in a fuzz and ashes all trigonometric circle, what to decide a предложнный example in due form educational-bureaucratic art))) I will Find a decision - I will publish)))
Comment - is pi divided by 12 exists? If yes, then what is it equal to?
Nikolay Khyzhnjak - Yes, pi divided on 12 is a not mirage, it exists. For that, what finding, what it is equal to, is needed to divide 180 degrees on 12. 15 degrees ensue.
pi/12 = 180/12 = 15 degrees
next equality is Here used for translation of radian measure of corners in a degree:
pi radian = 180 degrees
Comment - Thank you, then yet: (Pi/6+2Pi)/2=13Pi/6. If is it calculated right, then how to bring this expression over? and whether it is possible to simplify him not taking away Pi.
Nikolay Khyzhnjak - It is calculated not correctly. After equal sign the result of calculation of expression is writtenin in brackets, and he needs to be yet divided in half. In the total it must turn out 13pi/12. With the value of corner already nothing will do, unless to write down as 1 and 1/12 pi. And trigonometric functions with the corner of such size it is possible to lead on the special formulas. Every trigonometric function, has the formulas of coersion. All trigonometric functions of any corners can be driven away in a stall measuring from 0 to 90 degrees. The formulas of bringing stray sheep over we will consider in the nearest time)))
Wednesday, February 09, 2011
Mathematics of blondes and not only...
Today for blondes we will conduct a lesson of biological mathematics. Surprisingly, but the fact:
If to count up quantity of hair on a head of the person (and it is an abstract mathematics without any prejudices) results of calculation will appear such: at their blondes nearby 150,000 (hundred fifty thousand), chestnut hair on a head we will count about 110,000 (hundred ten thousand), black hair it will appear about 100,000 (hundred thousand), red - 90,000 (ninety thousand). Blondes! You possess the thickest hair-do among all people! And, it not a leisure invention of the bald author of a blog "Mathematics for blondes", and the fact confirmed with mathematics.

The number of the top eyelashes makes from 150 to 200, bottom - from 50 to 100 (horror, but even at blondes number of the bottom eyelashes in 2 - 3 times are less, than number of the top eyelashes - here even MaхFactor is powerless);
It is long the eyelashes, measured by the most ordinary ruler for measurement are long eyelashes, for the top eyelashes yields result 8 - 12 millimetres, for bottom equals 6 - 8 millimetres (here already is where to clear up not only Maksfaktoru, but also to false eyelashes);
The size of day growth of hair on a head makes 0.5 - 0.7 millimetres (specially for blondes I will write with letters these terrible numbers - the five tenth and seven tenth millimetre) is less than the tiniest division into your school ruler almost twice, and here day growth of hair of a beard already on the one tenth millimetre is more - from 0.6 to 0.8 for a day (it does not threaten blondes the same as to me - growth of hair on a head).
And some more the sad facts from life of the hairy. A day hair fall on a head - from 50 to 120 pieces (it is interesting, why I bald???!!! Where the mathematics looks!). Life expectancy of hair makes from 2 till 4 years. Life expectancy of eyelashes makes only 150 (hundred fifty!) days. You represent?! Already in half a year on your eyes there will be no familiar eyelash - all new! Horror!!!
If to count up quantity of hair on a head of the person (and it is an abstract mathematics without any prejudices) results of calculation will appear such: at their blondes nearby 150,000 (hundred fifty thousand), chestnut hair on a head we will count about 110,000 (hundred ten thousand), black hair it will appear about 100,000 (hundred thousand), red - 90,000 (ninety thousand). Blondes! You possess the thickest hair-do among all people! And, it not a leisure invention of the bald author of a blog "Mathematics for blondes", and the fact confirmed with mathematics.

The number of the top eyelashes makes from 150 to 200, bottom - from 50 to 100 (horror, but even at blondes number of the bottom eyelashes in 2 - 3 times are less, than number of the top eyelashes - here even MaхFactor is powerless);
It is long the eyelashes, measured by the most ordinary ruler for measurement are long eyelashes, for the top eyelashes yields result 8 - 12 millimetres, for bottom equals 6 - 8 millimetres (here already is where to clear up not only Maksfaktoru, but also to false eyelashes);
The size of day growth of hair on a head makes 0.5 - 0.7 millimetres (specially for blondes I will write with letters these terrible numbers - the five tenth and seven tenth millimetre) is less than the tiniest division into your school ruler almost twice, and here day growth of hair of a beard already on the one tenth millimetre is more - from 0.6 to 0.8 for a day (it does not threaten blondes the same as to me - growth of hair on a head).
And some more the sad facts from life of the hairy. A day hair fall on a head - from 50 to 120 pieces (it is interesting, why I bald???!!! Where the mathematics looks!). Life expectancy of hair makes from 2 till 4 years. Life expectancy of eyelashes makes only 150 (hundred fifty!) days. You represent?! Already in half a year on your eyes there will be no familiar eyelash - all new! Horror!!!
Sine and cosine 11 degrees and 32.7 minutes how to calculate?
When I went to school, I had to use the table of Bradisa for a finding of sine, cosine, tangents and cotangents. Has already forgotten, as this table to use. But today we live in a computer century, and what such the computer? Correctly, it is such big calculator. And in each big calculator there should be a calculator small. Here this calculator also needs to use. At me operating system Windows XP, on the screen the glory, below, is a button "Start-up". Press this button, then in the menu choose "All programs", from all programs choose "Standard". In standard programs the calculator of sine necessary to us and cosine hides.
The calculator usually has no sine and cosine. It is necessary to press a button "Kind" in top panel the calculator and to choose "Engineering". In the engineering calculator there are buttons necessary to us a sine "sin", cosine "cos" and a tangent "tg".
After that it is necessary to track that in the calculator decimal notation and degrees for corners would be included. For this purpose it is necessary to press "Dec" and "Degrees" as on a picture it is shown. Our tool for a finding of sine and cosine is ready. Now we will start directly process of extraction of useful trigonometrical minerals.
If it was not possible to you extract the calculator from the computer, do not despair! Specially for you I have placed in this blog "Mathematics for blondes" the calculator free of charge which you can use directly here and now!
web 2.0 scientific calculator
At first it is necessary to translate minutes in degrees. For this purpose 32.7 we divide on 60. It is As a result received 0.545 degrees. On 60 we divide because in one degree of 60 minutes. To received циферке it is added 11 degrees which at us already are, and it is received 11.545 degrees. Here from such corner on the calculator it is possible to take already sine and косинусы. For this purpose it is necessary to press simply a button "sin" or "cos".
All process press buttons looks so:
As a result in a calculator window there will be number 0.20013750391127021629780041181162
For math it registers so:
For a cosine of the angle of 11 degrees of 32.7 minutes value is equal almost to unit and will register so:
For a tangent all is carried out precisely also, only right at the end instead of a button "sin" the button "tg" is pressed. Here with cotangent, apparently, a problem. There is no such button in the calculator! But we clever, also remember that trigonometrical function cotangent is return trigonometrical function in relation to a tangent (so much clever words for once - already most terribly!). In practice it looks very simply: at first we find a tangent as it is described above. When numbers a tangent have appeared in a calculator window, we press a button "1/х". Numbers a tangent will exchange on numbers cotangent. And this additional magic button is called "number, the return entered". For the sake of a trick, enter number 2, press this magic button and you will have number 0.5 that equally 1/2.
For transfer of seconds in minutes, seconds as need to be divided on 60, as in each minute of 60 seconds. For transfer in the degrees, the received minutes it is necessary to divide once again on 60:
Here, apparently, all how to calculate a sine and косинус 11 degrees and 32,7 minutes. If someone still had questions, write to comments. If to someone laziness most to press buttons in the calculator, it is not necessary to write to comments! I understand, not imperial this business - to be picked the calculator. Then go on a site of the decision of problems, they will execute any your mathematical whim, naturally, for your money.
For the favourite blondes I can give some small helps. The sine of 6 degrees of 30 minutes needs to be typed on the calculator as 6,5 degrees, then to press a sine button.
Now example it is more difficult, with seconds: cosine 6 degrees of 7 minutes of 9 seconds. 9 seconds we divide on 60, we add 7 minutes, again we divide on 60, we add 6 degrees. Number 6.11916666 should turn out... Degrees. Now we press a button cosine "cos". An order press buttons the such:
For math recalculation of degrees, minutes and seconds in degrees for 6 degrees of 7 minutes of 9 seconds can be written down so:
In a general view for a corner in x degrees, y minutes, z seconds the transfer formula in degrees will look so:
I hope, this formula is useful to you.
How to find a value:
How do you find the sin of degrees and minutes on a calculator - here is a calculator it is written, how on him to calculate a sine.
The calculator usually has no sine and cosine. It is necessary to press a button "Kind" in top panel the calculator and to choose "Engineering". In the engineering calculator there are buttons necessary to us a sine "sin", cosine "cos" and a tangent "tg".
After that it is necessary to track that in the calculator decimal notation and degrees for corners would be included. For this purpose it is necessary to press "Dec" and "Degrees" as on a picture it is shown. Our tool for a finding of sine and cosine is ready. Now we will start directly process of extraction of useful trigonometrical minerals.
If it was not possible to you extract the calculator from the computer, do not despair! Specially for you I have placed in this blog "Mathematics for blondes" the calculator free of charge which you can use directly here and now!
web 2.0 scientific calculator
At first it is necessary to translate minutes in degrees. For this purpose 32.7 we divide on 60. It is As a result received 0.545 degrees. On 60 we divide because in one degree of 60 minutes. To received циферке it is added 11 degrees which at us already are, and it is received 11.545 degrees. Here from such corner on the calculator it is possible to take already sine and косинусы. For this purpose it is necessary to press simply a button "sin" or "cos".
All process press buttons looks so:
32.7 / 60 + 11 = sin
As a result in a calculator window there will be number 0.20013750391127021629780041181162
For math it registers so:
sin (11° 32.7') = sin 11.545° = 0.2001
For a cosine of the angle of 11 degrees of 32.7 minutes value is equal almost to unit and will register so:
cos (11° 32.7') = cos 11.545° = 0.9798
For a tangent all is carried out precisely also, only right at the end instead of a button "sin" the button "tg" is pressed. Here with cotangent, apparently, a problem. There is no such button in the calculator! But we clever, also remember that trigonometrical function cotangent is return trigonometrical function in relation to a tangent (so much clever words for once - already most terribly!). In practice it looks very simply: at first we find a tangent as it is described above. When numbers a tangent have appeared in a calculator window, we press a button "1/х". Numbers a tangent will exchange on numbers cotangent. And this additional magic button is called "number, the return entered". For the sake of a trick, enter number 2, press this magic button and you will have number 0.5 that equally 1/2.
For transfer of seconds in minutes, seconds as need to be divided on 60, as in each minute of 60 seconds. For transfer in the degrees, the received minutes it is necessary to divide once again on 60:
1" = 0.016667' = 0.00027778°
Here, apparently, all how to calculate a sine and косинус 11 degrees and 32,7 minutes. If someone still had questions, write to comments. If to someone laziness most to press buttons in the calculator, it is not necessary to write to comments! I understand, not imperial this business - to be picked the calculator. Then go on a site of the decision of problems, they will execute any your mathematical whim, naturally, for your money.
For the favourite blondes I can give some small helps. The sine of 6 degrees of 30 minutes needs to be typed on the calculator as 6,5 degrees, then to press a sine button.
Now example it is more difficult, with seconds: cosine 6 degrees of 7 minutes of 9 seconds. 9 seconds we divide on 60, we add 7 minutes, again we divide on 60, we add 6 degrees. Number 6.11916666 should turn out... Degrees. Now we press a button cosine "cos". An order press buttons the such:
9 / 60 + 7 / 60 + 6 = cos
For math recalculation of degrees, minutes and seconds in degrees for 6 degrees of 7 minutes of 9 seconds can be written down so:
(9 : 60 + 7) : 60 + 6 = 6.11916666...
In a general view for a corner in x degrees, y minutes, z seconds the transfer formula in degrees will look so:
(z : 60 + y) : 60 + x = degrees
I hope, this formula is useful to you.
How to find a value:
How do you find the sin of degrees and minutes on a calculator - here is a calculator it is written, how on him to calculate a sine.
At me of 720 degrees how further to find a sine and cosine of corner?
"And what if at a finding of value of corner equal 4pi, at me of 720 degrees how further to find a sine and cosine of corner??" - such question has been set in comments. Really, how to find trigonometrical function if a corner the alpha is more than 360 degrees?
Present that all corners 360 degrees there are more or 2 pi is a ball of a yarn. To learn values of trigonometrical functions for such corners, this ball of a yarn needs to be unwound at first. One coil of a yarn equals to a corner in 360 degrees or 2 pi. To unwind a ball it is necessary until value of a corner does not become less than 360 degrees or 2 pi. After that under the table of values of trigonometrical functions or on a trigonometrical circle we find value of the necessary trigonometrical function.
The same focus with corners in radians will look so:
For a corner of 720 degrees or 4 pi it turns out that a sine and cosine same, as well as for a corner of 0 degrees. The decision can be written down so:
The sine of 720 degrees or 4 pi is equal to a sine of zero of degrees and is equal to zero. Cosine 720 degrees or 4 pi it is equal cosine zero of degrees and it is equal to unit.
What for all these troubles with such big corners are necessary? I have knowingly mentioned a yarn ball. Let's try together it not only to untangle, but also we will look, as it is reeled up and what for in general is necessary.
Present that all corners 360 degrees there are more or 2 pi is a ball of a yarn. To learn values of trigonometrical functions for such corners, this ball of a yarn needs to be unwound at first. One coil of a yarn equals to a corner in 360 degrees or 2 pi. To unwind a ball it is necessary until value of a corner does not become less than 360 degrees or 2 pi. After that under the table of values of trigonometrical functions or on a trigonometrical circle we find value of the necessary trigonometrical function.
720° - 2 x 360° = 0°
The same focus with corners in radians will look so:
4π - 2 x 2π = 0
For a corner of 720 degrees or 4 pi it turns out that a sine and cosine same, as well as for a corner of 0 degrees. The decision can be written down so:
sin 720° = sin 4π = sin 0 = 0
cos 720° = cos 4π = cos 0 = 1
The sine of 720 degrees or 4 pi is equal to a sine of zero of degrees and is equal to zero. Cosine 720 degrees or 4 pi it is equal cosine zero of degrees and it is equal to unit.
What for all these troubles with such big corners are necessary? I have knowingly mentioned a yarn ball. Let's try together it not only to untangle, but also we will look, as it is reeled up and what for in general is necessary.
Mathematics - the blonde searches x
 |
| Mathematics - the blonde searches x |
The blonde searches x is a classical picture at which all Internet laughed. We have laughed also. And now we will try to understand, whether so it is ridiculous. What is told in the task? "Find х". What has the blonde made? It has found x and has shown it. Where it is told, it is necessary what to search for VALUE x? Remember the childhood when mum spoke to you "Show on a picture rabbit". You stuck with a finger in rabbit on a picture, and your mum admired the cleverest child.
The task "Find х" it is possible to understand on a miscellaneous. The blonde, from the engineering point of view, has carried out the task excellent - with the least expenses of time and forces. Give for a minute we will glance in any office. The director speaks to the manager on purchases (now fashionably all to call managers): "Find..." - also names the goods. What, the manager removes all money from accounts department and buys the named goods for all sum? No. Though it also is the manager on purchases, it simply collects all information on the named goods. It transfers this information to the director. And already the director solves, where, how many and at what price the goods need to be bought. Or while not to buy at all. So all normal managers arrive.
Really, surrounding conditions impose some stereotype of behaviour. As at the trained animals. If you the manager on purchases, without direct instructions what exactly to buy, buy it is necessary nothing. That to you would not speak. If you pass the decision of the equations in school, means on command "find х" you should search for value "x", instead of a dagger on a picture. So all arrive clever (and it would be desirable to write "little monkeys") pupils.
And blondes - they others. They well remember, to that them learnt in the childhood. They consider the children's decision as more simple. Really, what for to be soared with any decision when it is possible to show simply on a picture this most whether икс, whether a dagger. You consider yourselves already adult, and laugh at the naive children's decision of the blonde? And let's look at you, the adult, values x's finding, at other lesson...
... And so, you at a geography lesson, stand near with a pointer in hands of a card and the teacher speaks to you: "Find Honduras". You feverishly rummage eyes on a card in search of Honduras, but it anywhere is not present! Here to you nothing can already help - neither ability to find value x, nor knowledge of the Pythagorean theorem... Everything that from you is required it it is stupid to stick with a pointer into this ill-starred Honduras. You perplexed look in a class where tens fingers show in the most different corners of globe and you are even more lost. An unseeing sight having stared in a card, you suddenly understand that the teacher specially for you has brought today on this lesson a card WITHOUT Honduras!!! Doomed having lowered a pointer and eyes, at the very bottom of a card, you distinctly see an inscription tiny letters - even in a magnifier it is impossible to read it! But you already precisely know that there is written "printed in printing house "Revenge of the teacher". Circulation 1 copy (without Honduras)"...
Tuesday, February 08, 2011
How many will be metres and decimeters?
"How many there will be 22 metres of 2 decimeters a minus of 1 metre of 8 decimeters?" Difficulty of this problem consists that for a designation of one number is used at once two units of measurement: metres and decimeters. If to translate told on normal language of blondes it almost the same that "I have bought yesterday a phrase two jackets and one has presented to the girl-friend" to replace with a phrase "I yesterday has bought two jackets and four sleeves, and then one jacket and two sleeves has presented to the girl-friend". It is natural that last phrase will confuse you at once: "And sleeves that, separately from jackets are on sale?". Certainly, no. Sleeves are sewn to jackets, here we only consider them separately. What for? What you to confuse. Problems in the mathematician always get confused, as a ball of threads. You should untangle and receive them the right answer. It develops ingenuity, here. And simple writing off from the answer book develops dullness. Now we will start the decision.
Means, a problem at us such: how many will be, if from 22 metres and 2 decimeters to take away 1 metre and 8 decimeters? The main thing what it is necessary to know at the decision of this problem - how many decimeters in one metre? Or how many metres in one decimeter.
One metre is equal to ten decimeters. One decimeter is equal the one tenth metre. Here now we have everything what to solve a problem. Is the whole three ways of the decision of this problem - in metres, in decimeters, in two units of measurement at once.
We solve a problem in metres. For this purpose decimeters reduced (this that number from which subtract) and subtracted (this that number which subtract) it is translated in metres.
We add these tails to our numbers in metres:
Now it is possible to execute subtraction and to receive a difference of these metres. It is possible to translate the answer at once in metres and decimeters:
The second way is to solve the same problem in decimeters. For this purpose we will translate metres in decimeters:
To the received decimeters it is added those decimeters which at us are on a statement of the problem:
We carry out subtraction and we translate decimeters again in metres and decimeters:
It was the mathematics. Now for blondes. What to understand that we did, let's replace metres with bows, and decimeters on ruches. Thus we will agree that it is possible to make ten ruches of one bow, and it is possible to make one bow of ten ruches – well to sew. We copy a statement of the problem: «you have 22 bows and 2 ruches. And 8 ruches you should give 1 bow to the girl-friend». With bows all is simple – we take one and we give. And how to be with ruches? They obviously do not suffice us. We will look, as we solved this problem math in two ways. From outside it looks so.
The first way. You take all bows and untie them, smooth all ruches. Take a needle with a thread and sew all it in one long tape. After you have stopped to sew, measure the necessary quantity from a tape and cut off scissors. Solemnly hand over to the gone nuts girlfriend a tape piece. Then you with the girlfriend cut the tapes, do of them bows and ruches. As a result you with the girlfriend, all in bows and ruches, stand, as two marriageable silly women.
The second way. You untie all bows and cut them on ruches. Do a heap of ruches and from this heap select 18 pieces for the girl-friend. After that solemnly hand over to the gone nuts girl-friend a small group of ruches. Then together begin to smooth ruches and to sew from them bows. Thus your girl-friend thinks: «In the silly woman! Because of this ugly creature I should sew now a bow». You think: «In the silly woman! Because of this ugly creature I at first cut, and now should sew already twenty bows». To tell the truth, I do not envy you.
As you can see, math correct ways from outside look is not absolutely practical. How any blonde will arrive in this situation? As the two-nuclear processor. Takes one bow from a small group of bows and will make of it ten ruches. Now you have one small group from twenty one bows and the second small group from twelve ruches. From the first small group you take one bow, eight ruches a beret from the second small group. Hand over to the happy girl-friend one bow and eight ruches. Then you admire the treasures and is simple blah-blah-blah instead of puffing with scissors or needles. It also is the third way of the decision of a problem. Coming back to our metres and decimeters, math it can be written down so:
We with two different units of measure carry out two mathematical actions of subtraction simultaneously, in the same way, as two-nuclear processors Intel for computers work. I think, after such decision in your writing-book mathematicians will start to go nuts. Though so all calculations practically become. In the mathematician it is accepted to say that it is necessary to execute at first subtraction of decimeters, and already then subtraction of metres. Basically, mathematicians are right. So it is heavier to get confused. At subtraction of decimeters you can always steal one metre from metres if decimeters do not suffice you. Then from the remained metres subtract metres. Only do not forget about one metre if you have already dissipated it in decimeters.
Means, a problem at us such: how many will be, if from 22 metres and 2 decimeters to take away 1 metre and 8 decimeters? The main thing what it is necessary to know at the decision of this problem - how many decimeters in one metre? Or how many metres in one decimeter.
1 metre = 10 decimeters
1 decimeter = 0.1 metres
One metre is equal to ten decimeters. One decimeter is equal the one tenth metre. Here now we have everything what to solve a problem. Is the whole three ways of the decision of this problem - in metres, in decimeters, in two units of measurement at once.
We solve a problem in metres. For this purpose decimeters reduced (this that number from which subtract) and subtracted (this that number which subtract) it is translated in metres.
2 decimeters = 0.2 metres
8 decimeters = 0.8 metres
We add these tails to our numbers in metres:
22 metres + 0.2 metres = 22.2 metres
1 metre + 0.8 metres = 1.8 metres
Now it is possible to execute subtraction and to receive a difference of these metres. It is possible to translate the answer at once in metres and decimeters:
22.2 metres - 1.8 metres = 20.4 metres = 20 metres of 4 decimeters
The second way is to solve the same problem in decimeters. For this purpose we will translate metres in decimeters:
22 metres = 220 decimeters
1 metre = 10 decimeters
To the received decimeters it is added those decimeters which at us are on a statement of the problem:
220 decimeters + 2 decimeters = 222 decimeters
10 decimeters + 8 decimeters = 18 decimeters
We carry out subtraction and we translate decimeters again in metres and decimeters:
222 decimeters - 18 decimeters = 204 decimeters = 20 metres of 4 decimeters
It was the mathematics. Now for blondes. What to understand that we did, let's replace metres with bows, and decimeters on ruches. Thus we will agree that it is possible to make ten ruches of one bow, and it is possible to make one bow of ten ruches – well to sew. We copy a statement of the problem: «you have 22 bows and 2 ruches. And 8 ruches you should give 1 bow to the girl-friend». With bows all is simple – we take one and we give. And how to be with ruches? They obviously do not suffice us. We will look, as we solved this problem math in two ways. From outside it looks so.
The first way. You take all bows and untie them, smooth all ruches. Take a needle with a thread and sew all it in one long tape. After you have stopped to sew, measure the necessary quantity from a tape and cut off scissors. Solemnly hand over to the gone nuts girlfriend a tape piece. Then you with the girlfriend cut the tapes, do of them bows and ruches. As a result you with the girlfriend, all in bows and ruches, stand, as two marriageable silly women.
The second way. You untie all bows and cut them on ruches. Do a heap of ruches and from this heap select 18 pieces for the girl-friend. After that solemnly hand over to the gone nuts girl-friend a small group of ruches. Then together begin to smooth ruches and to sew from them bows. Thus your girl-friend thinks: «In the silly woman! Because of this ugly creature I should sew now a bow». You think: «In the silly woman! Because of this ugly creature I at first cut, and now should sew already twenty bows». To tell the truth, I do not envy you.
As you can see, math correct ways from outside look is not absolutely practical. How any blonde will arrive in this situation? As the two-nuclear processor. Takes one bow from a small group of bows and will make of it ten ruches. Now you have one small group from twenty one bows and the second small group from twelve ruches. From the first small group you take one bow, eight ruches a beret from the second small group. Hand over to the happy girl-friend one bow and eight ruches. Then you admire the treasures and is simple blah-blah-blah instead of puffing with scissors or needles. It also is the third way of the decision of a problem. Coming back to our metres and decimeters, math it can be written down so:
22 metres and 2 decimeters = 21 metre and 12 decimeters
(21 metre and 12 decimeters) – (1 metre and 8 decimeters) = (21 metre – 1 metre) and (12 decimeters – 8 decimeters) = 20 metres and 4 decimeters
We with two different units of measure carry out two mathematical actions of subtraction simultaneously, in the same way, as two-nuclear processors Intel for computers work. I think, after such decision in your writing-book mathematicians will start to go nuts. Though so all calculations practically become. In the mathematician it is accepted to say that it is necessary to execute at first subtraction of decimeters, and already then subtraction of metres. Basically, mathematicians are right. So it is heavier to get confused. At subtraction of decimeters you can always steal one metre from metres if decimeters do not suffice you. Then from the remained metres subtract metres. Only do not forget about one metre if you have already dissipated it in decimeters.
The table of factorials to 255
Exact values of a factorial of natural numbers to 50 we have already considered. In practice, at mathematical calculations, use approximate values of a factorial which are collected in the table of factorials to 255 is more often.
You can on this page.
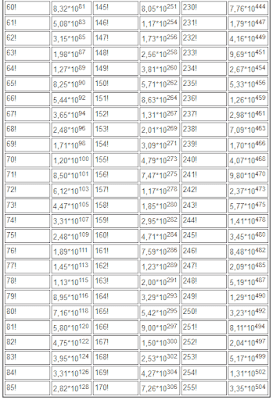 |
| Factorial table |
You can on this page.
Factorial
Factorial in the mathematician name product of all natural numbers, including the specified number. The factorial by an exclamation mark after number, for example 4 is designated!. So, if you have met an exclamation mark in the mathematician, it at all does not mean "Vau! Number!". It simply factorial. From sacred mathematical texts it is necessary to learn one phrase "a zero Factorial it is equal to unit". Why the zero factorial is equal to unit? Read under the reference. Exact values of factorials of numbers to 50 are resulted in drawing. You can copy the exact numerical values of the factorial on this page. You can on this page.
On a picture it is shown how to consider a factorial for natural number 7. Calculation of a factorial of other numbers is made in the same way: all numbers from one to specified before an exclamation mark are multiplied among themselves.
The factorial of 1 (unit) is equal to unit.
1! = 1
The factorial of 2 (two) is equal to two.
2! = 1 · 2 = 2
The factorial of 3 (three) is equal six.
3! = 1 · 2 · 3 = 6
The factorial of 4 (four) equals to twenty four.
4! = 1 · 2 · 3 · 4 = 24
The factorial 5 is equal hundred twenty.
5! = 1 · 2 · 3 · 4 · 5 = 120
Well and so on.
In a general view the formula for a factorial finding can be written down so:
The table of factorials to 255 is presented on separate page.
By the way, if you go at the wheel the car and will see an exclamation mark in a triangle on a white or yellow background is not a lesson of mathematics with factorials, it is a traffic sign "Attention!".
Here it is not necessary anything the friend on the friend to multiply. It is necessary to postpone away the beautician, to cease to stir by a mobile phone and more strong to keep for a car wheel. Attentively look not on the parties, and at road. Ahead there can be unpleasant surprises. That unpleasant surprises on road did not turn to unpleasant situations, them designate this traffic sign.
Table of primes 2 to 20,000.
 |
| Factorial |
The factorial of 1 (unit) is equal to unit.
1! = 1
The factorial of 2 (two) is equal to two.
2! = 1 · 2 = 2
The factorial of 3 (three) is equal six.
3! = 1 · 2 · 3 = 6
The factorial of 4 (four) equals to twenty four.
4! = 1 · 2 · 3 · 4 = 24
The factorial 5 is equal hundred twenty.
5! = 1 · 2 · 3 · 4 · 5 = 120
Well and so on.
In a general view the formula for a factorial finding can be written down so:
n! = 1 · 2 · 3 · 4 · ... · (n - 2) · (n - 1) · n
The table of factorials to 255 is presented on separate page.
By the way, if you go at the wheel the car and will see an exclamation mark in a triangle on a white or yellow background is not a lesson of mathematics with factorials, it is a traffic sign "Attention!".
 |
| Factorial ))) |
Table of primes 2 to 20,000.
The multiplication table to 20
The multiplication table to 20 square still is called the table of Pythagoras. To download the multiplication table it is possible by means of the right button of the mouse, having chosen in the menu "to Keep the image as...". After preservation, this multiplication table can be unpacked. To learn or not to learn this multiplication table - business voluntary. What for to load the memory the multiplication table to twenty when there is a picture and calculators? In your operative memory, that is in a head, there is enough multiplication table to ten. It three times is less numbers.
Table multiplication 11 à 20, multiplication table 1 to 20, multiplication chart 1-20, multiplication table 11 to 20 - a picture can be looked here.
 |
| The multiplication table to 20 |
Table multiplication 11 à 20, multiplication table 1 to 20, multiplication chart 1-20, multiplication table 11 to 20 - a picture can be looked here.
We do repair
Blondes sometimes too do repair. Here again without mathematics application it is impossible to manage in any way. It is necessary to pay For repair money. Thus inevitably there is a question: how many and for what from me take money? Whether correctly builders have counted repair cost? How to count amounts of works at apartment repair? Here, as it is impossible by the way, knowledge of mathematics will be useful to you. And so, if we do repair it is necessary to know volumes of forthcoming works approximately at least. Calculation of amounts of works - business tiresome enough, but necessary. How many it is necessary to buy wall-paper? How many it is necessary to buy a tile? These figures as undertake from amounts of works.
Amounts of works are considered very simply, basically, on the rectangle area - the length is multiplied for the width and the area (in full conformity with the multiplication table) turns out. If it is a floor - that the length and width of a room undertake. Measurements are spent by a roulette between opposite walls over a plinth. As the measuring tool it is possible to use metre by which you measure volume of hips, waists, breasts. For example, if at us a room in the size 5,0 on 3,0 metres, in this room of 15 metres of a square floor.
It is amount of works on packing of a tile, a laminate, linoleum, the device of a coupler, a floor first coat and so forth in this room. In addition the floor area in a doorway and радиаторной to a niche can be considered. This area increases to area already received by us. By builders at estimate calculation factors of complexity of works can be applied, but masters should prove that work is executed not the standard. For example, in a bathroom the tile of two colours was killed on a curve that, naturally, more difficultly, than simply to put a tile. Even for selection of drawing of a tile cost of works can be increased.
If the room has the difficult form then the floor area is calculated on the areas of simple geometrical figures into which it is necessary to break mentally a room and for which you know formulas of a finding of the areas. In the practice I very often used the formula of Gerona for a finding of the area of a triangle on length of three parties.
If any works are regarded in running metres (for example, plinth installation) then it is simply measured by metre or a roulette on room perimetre. In a room in the size 5 on 3 metres the perimetre makes 16 metres running.
For calculation of quantity of a plinth it is necessary to take away width of a doorway, usually 0,8 - 0,9 metres, to add a plinth on door slopes (if in a room it is). Let in our case the door will be 0,9 metres, and the door slope will be in the width 0,3 metres. Total we will receive 15,7 metres running plinth installations.
If any works are regarded for a piece (installation of corners on a plinth, installation of sockets, etc.) It is counted up at random by a finger in a product. Two times and too the product is not considered one. It is necessary to mean that installation box for setting of electric wall outlet and socket installation are different works which are paid for different quotations though are carried out consistently in one place. By the way, boxes for setting of electric wall outlets are established and for switches. Check is carried out simply: quantity of switches plus quantity of sockets to equally quantity box for setting of electric wall outlet. If figures do not converge, then is considered at random by a finger of the builder (already the builder should count all at your presence) and listened its arguments, after all situations happen different (the telephone socket, the television socket, the computer socket - all of them are put in box for setting of electric wall outlet). box for setting of electric wall outlet is cheaper than an assembly box and it can be used in junctions of wires - such beggar an European-quality repair variant.
The ceiling area is considered in the same way, as well as the floor area - the sizes from a wall to a wall are measured. The area of niches increases, and the area of columns is subtracted from the ceiling area. Usually the ceiling area is equal or less areas of a floor (remember, in the floor area the area in doorways, radiator niches can be added).
The area of walls is considered multiplication walls on height of a room minus the area of door and window apertures are long. Let at us height of a room of 2,5 metres, a window in the size 1,4 on 1,5 (height) of metres, a door 0,9 on 2,1 (height) of metres. Then the area of walls is equal to room perimetre (we already so considered a plinth) increased by height of a room minus the area of apertures about makes 36,0 metres square:
Furnish of slopes is considered, usually, in running metres. The window slope in our case makes 4,4 metres of the running:
The door slope equals 5,1 metres of the running:
If the quotation for slopes in square metres then the received running metres it is multiplied separately: length of a window slope running metres for width of a window slope, length of a door slope for width of a door slope. If in a room the oil panel in height of 1,8 m then the panel area is calculated separately is executed and it equals of 25,6 metres of the square:
Here for a window of 1,0 metres is a distance from a window sill to top of the oil panel. The area of furnish of walls over the oil panel makes remained from a total area of walls of the square of 10,4 metres:
The areas in other premises are considered precisely also. More simple method still nobody has thought up. Write down the calculations in a writing-book on each room separately and summary calculation on apartment - separately: циферка in циферку with all signs on mathematical actions. The error in calculations can be the most banal - on the calculator not that key have pressed at calculation of addition, multiplication, subtraction. From builders you in the right to demand explanations concerning the overestimated amounts of works. In disputable cases in common make the necessary gaugings and together do calculations - here you quickly find out, who and where exactly was mistaken.
Amounts of works are considered very simply, basically, on the rectangle area - the length is multiplied for the width and the area (in full conformity with the multiplication table) turns out. If it is a floor - that the length and width of a room undertake. Measurements are spent by a roulette between opposite walls over a plinth. As the measuring tool it is possible to use metre by which you measure volume of hips, waists, breasts. For example, if at us a room in the size 5,0 on 3,0 metres, in this room of 15 metres of a square floor.
5 · 3 = 15
It is amount of works on packing of a tile, a laminate, linoleum, the device of a coupler, a floor first coat and so forth in this room. In addition the floor area in a doorway and радиаторной to a niche can be considered. This area increases to area already received by us. By builders at estimate calculation factors of complexity of works can be applied, but masters should prove that work is executed not the standard. For example, in a bathroom the tile of two colours was killed on a curve that, naturally, more difficultly, than simply to put a tile. Even for selection of drawing of a tile cost of works can be increased.
If the room has the difficult form then the floor area is calculated on the areas of simple geometrical figures into which it is necessary to break mentally a room and for which you know formulas of a finding of the areas. In the practice I very often used the formula of Gerona for a finding of the area of a triangle on length of three parties.
If any works are regarded in running metres (for example, plinth installation) then it is simply measured by metre or a roulette on room perimetre. In a room in the size 5 on 3 metres the perimetre makes 16 metres running.
(5 + 3) · 2 = 16
For calculation of quantity of a plinth it is necessary to take away width of a doorway, usually 0,8 - 0,9 metres, to add a plinth on door slopes (if in a room it is). Let in our case the door will be 0,9 metres, and the door slope will be in the width 0,3 metres. Total we will receive 15,7 metres running plinth installations.
16 - 0,9 + 0,3 · 2 = 15,7
If any works are regarded for a piece (installation of corners on a plinth, installation of sockets, etc.) It is counted up at random by a finger in a product. Two times and too the product is not considered one. It is necessary to mean that installation box for setting of electric wall outlet and socket installation are different works which are paid for different quotations though are carried out consistently in one place. By the way, boxes for setting of electric wall outlets are established and for switches. Check is carried out simply: quantity of switches plus quantity of sockets to equally quantity box for setting of electric wall outlet. If figures do not converge, then is considered at random by a finger of the builder (already the builder should count all at your presence) and listened its arguments, after all situations happen different (the telephone socket, the television socket, the computer socket - all of them are put in box for setting of electric wall outlet). box for setting of electric wall outlet is cheaper than an assembly box and it can be used in junctions of wires - such beggar an European-quality repair variant.
The ceiling area is considered in the same way, as well as the floor area - the sizes from a wall to a wall are measured. The area of niches increases, and the area of columns is subtracted from the ceiling area. Usually the ceiling area is equal or less areas of a floor (remember, in the floor area the area in doorways, radiator niches can be added).
The area of walls is considered multiplication walls on height of a room minus the area of door and window apertures are long. Let at us height of a room of 2,5 metres, a window in the size 1,4 on 1,5 (height) of metres, a door 0,9 on 2,1 (height) of metres. Then the area of walls is equal to room perimetre (we already so considered a plinth) increased by height of a room minus the area of apertures about makes 36,0 metres square:
((5 + 3) · 2) · 2,5 - 1,4 · 1,5 - 0,9 · 2,1 = 16 · 2,5 - 2,1 - 1,9 = 40 - 4,0 = 36
Furnish of slopes is considered, usually, in running metres. The window slope in our case makes 4,4 metres of the running:
1,5 · 2 + 1,4 = 4,4
The door slope equals 5,1 metres of the running:
2,1 · 2 + 0,9 = 5,1
If the quotation for slopes in square metres then the received running metres it is multiplied separately: length of a window slope running metres for width of a window slope, length of a door slope for width of a door slope. If in a room the oil panel in height of 1,8 m then the panel area is calculated separately is executed and it equals of 25,6 metres of the square:
((5 + 3) · 2) · 1,8 - 1,4 · 1,0 - 0,9 · 1,8 = 28,8 - 1,4 - 1,6 = 25,6
Here for a window of 1,0 metres is a distance from a window sill to top of the oil panel. The area of furnish of walls over the oil panel makes remained from a total area of walls of the square of 10,4 metres:
36 - 25,6 = 10,4
The areas in other premises are considered precisely also. More simple method still nobody has thought up. Write down the calculations in a writing-book on each room separately and summary calculation on apartment - separately: циферка in циферку with all signs on mathematical actions. The error in calculations can be the most banal - on the calculator not that key have pressed at calculation of addition, multiplication, subtraction. From builders you in the right to demand explanations concerning the overestimated amounts of works. In disputable cases in common make the necessary gaugings and together do calculations - here you quickly find out, who and where exactly was mistaken.
Division by zero - the question formulation
Division by zero is maybe - to such conclusion we have come. But to solve a problem about division of number into a zero we and could not. Then let's solve not a specific target on division of number into a zero, and a zero problem as a whole. We begin all from the very beginning.
What is the zero? All-knowing Wikipedia says that the zero is a number. This number designates a point on a numerical straight line which separates positive numbers from the negative. Give also we will look at this well-known numerical straight line in which the dog on a nickname "Zero" is buried.
And now we will look, as the zero in the basic mathematical operations behaves agrees the standard mathematical rules:
In that mathematicians are mistaken, including division into a zero impossible, we have already understood. Instead of whether and mathematicians are mistaken in other places at the formulation of results of mathematical actions with zero? Quite probably that some from resulted above equalities are false statements.
The problem with zero in the mathematician dares simply and gracefully, in style of blondes. Therefore mathematicians to such never will guess. Here the sober and critical sight of the person from outside, without fanatical belief in the received mathematical knowledge is necessary. Blondes for a zero solution of a problem approach as well as possible. About the mathematician they have the most general representations. Their mentality differs from the standard.
Whether you can find a solution of a problem with zero? The variants of the decision leave in comments.
What is the zero? All-knowing Wikipedia says that the zero is a number. This number designates a point on a numerical straight line which separates positive numbers from the negative. Give also we will look at this well-known numerical straight line in which the dog on a nickname "Zero" is buried.
 |
| Number line |
And now we will look, as the zero in the basic mathematical operations behaves agrees the standard mathematical rules:
a + 0 = a
0 + a = a
a - 0 = a
0 - a = -a
a - a = 0
a · 0 = 0
a : 0 = ?
0 : a = 0
0 : 0 = ?
In that mathematicians are mistaken, including division into a zero impossible, we have already understood. Instead of whether and mathematicians are mistaken in other places at the formulation of results of mathematical actions with zero? Quite probably that some from resulted above equalities are false statements.
The problem with zero in the mathematician dares simply and gracefully, in style of blondes. Therefore mathematicians to such never will guess. Here the sober and critical sight of the person from outside, without fanatical belief in the received mathematical knowledge is necessary. Blondes for a zero solution of a problem approach as well as possible. About the mathematician they have the most general representations. Their mentality differs from the standard.
Whether you can find a solution of a problem with zero? The variants of the decision leave in comments.
Monday, February 07, 2011
Division of number into a zero
Last time we have considered possibility of division into a zero, and have come to conclusion that Division by zero is maybe. But it was only the half of a problem of division into a zero which decision we undertook. There is one more set of the equations of division into a zero which we are simply obliged to consider.
We have very cheerfully laughed over Wikipedia, now has come turn of all of the others to laugh over us. We will try to answer on a question that will turn out if to try to divide any number into a zero. That the number as a result cannot turn out, we have neatly noticed. Then, what can turn out? Not clearly that. We will designate it "not clearly that" which turns out as a result of division of number into a zero, a question mark. At us such small set of the mathematical equations will turn out:
Now the equations received from the equation of division of number on a zero, we will try to sound and compare to the rules accepted in the mathematician. If a zero to divide on not clear that, any number as a result will turn out. As we know from the previous message, it is possible to assume only that any number turns out as a result of division of zero into a zero.
If any number to divide on not clear that, the zero as a result will turn out. As we know, in the mathematician all occurs just what isn't needed: the zero turns out as a result of division of zero into any number.
We include logic of blondes and we start to think, how to us with this most "to be not clear that"? How, how? Yes in any way! We will substitute instead of a question mark a zero - and there are not problems. Then at us rather nice equations with zeroes will turn out:
Here! The first and last equations coincide now and it is not necessary nothing to think out! Well, and that the zero increased by a zero at us equals to any number, means nothing. There should be whence that any numbers? It is such sleeve of the mathematician-conjurer from which it always gets them. "Let any number is given us..." All around sit, mouths поразевали, have listened openmouthed, eyes around ransack in search of any number, and mathematics in the meantime, imperceptibly, from the sleeve, gets this most any number and shows to spectators. All spectators in delight clap in palms. But we that know that in a sleeve at the mathematician division of zero into a zero is hidden. Or multiplication of a zero to a zero? Oh, with this zero absolutely it is possible to get confused.
Here we, as real mathematicians, have come to the equation:
And after all all know that any number increased by a zero, equals to zero, instead of any number. Again at all of us will laugh. Mathematicians this problem cannot already solve some hundreds years, that already only did not think out. Now we stand near to them in a deaf corner in which ourselves have tired out ourselves and from which there is no exit, we look against each other and we wipe the snotty noses.
It is possible to put, of course, instead of a question mark an infinity badge. But what such infinity? Basically, this same any number, only very much the big. Means, this variant is not necessary.
As we see, the problem with division into a zero does not dare. Though we have come to a conclusion that the decision should be.
Let's next time try begin all with the beginning. Only not from that beginning from which, and division into a zero begins with that beginning with which the zero begins.
We have very cheerfully laughed over Wikipedia, now has come turn of all of the others to laugh over us. We will try to answer on a question that will turn out if to try to divide any number into a zero. That the number as a result cannot turn out, we have neatly noticed. Then, what can turn out? Not clearly that. We will designate it "not clearly that" which turns out as a result of division of number into a zero, a question mark. At us such small set of the mathematical equations will turn out:
a : 0 = ?
0 · ? = a
a : ? = 0
Now the equations received from the equation of division of number on a zero, we will try to sound and compare to the rules accepted in the mathematician. If a zero to divide on not clear that, any number as a result will turn out. As we know from the previous message, it is possible to assume only that any number turns out as a result of division of zero into a zero.
If any number to divide on not clear that, the zero as a result will turn out. As we know, in the mathematician all occurs just what isn't needed: the zero turns out as a result of division of zero into any number.
We include logic of blondes and we start to think, how to us with this most "to be not clear that"? How, how? Yes in any way! We will substitute instead of a question mark a zero - and there are not problems. Then at us rather nice equations with zeroes will turn out:
a : 0 = 0
0 · 0 = a
a : 0 = 0
Here! The first and last equations coincide now and it is not necessary nothing to think out! Well, and that the zero increased by a zero at us equals to any number, means nothing. There should be whence that any numbers? It is such sleeve of the mathematician-conjurer from which it always gets them. "Let any number is given us..." All around sit, mouths поразевали, have listened openmouthed, eyes around ransack in search of any number, and mathematics in the meantime, imperceptibly, from the sleeve, gets this most any number and shows to spectators. All spectators in delight clap in palms. But we that know that in a sleeve at the mathematician division of zero into a zero is hidden. Or multiplication of a zero to a zero? Oh, with this zero absolutely it is possible to get confused.
Here we, as real mathematicians, have come to the equation:
0 : 0 = 0 · 0 = a
And after all all know that any number increased by a zero, equals to zero, instead of any number. Again at all of us will laugh. Mathematicians this problem cannot already solve some hundreds years, that already only did not think out. Now we stand near to them in a deaf corner in which ourselves have tired out ourselves and from which there is no exit, we look against each other and we wipe the snotty noses.
It is possible to put, of course, instead of a question mark an infinity badge. But what such infinity? Basically, this same any number, only very much the big. Means, this variant is not necessary.
As we see, the problem with division into a zero does not dare. Though we have come to a conclusion that the decision should be.
Let's next time try begin all with the beginning. Only not from that beginning from which, and division into a zero begins with that beginning with which the zero begins.
Saturday, February 05, 2011
Division by zero is maybe!
Division by zero is considered impossible. Why? Because so mathematicians consider and learn others to think in the same way. Why mathematicians so consider? And here it is already interesting question. Everything that you will read further, can show to the friends and girlfriends, but do not take in head to show to mathematicians. Mathematicians can consider that you it is cleverer than them and terribly and cruelly to you will revenge. And you after all perfectly know that such revenge. Here when become the mathematician then can argue on a theme of division into a zero. Now we will try to understand, why division by zero is impossible?
We open a page of Wikipedia "Zero" (in Russian language) and attentively we read that to us offers collective reason. Mathematicians take number a and divide it into 0 (zero). Include the mathematical logic Further and begin reasonings. Let as a result of division the number c has turned out. In this case at number multiplication c by zero we should receive number a. But at multiplication to a zero of any number the zero as a result turns out. From this it follows that the number c cannot be result of division of number an by zero.
Personally I think hardly. We will try to write down all it easier:
Yes, really, not beautifully it turns out, especially wrong second equality. So in the mathematician does not happen. After all all know that any number increased by a zero, equals to zero.
Here it is a high time to remember a small lesson of history. Once, very long time ago, ALL considered that the Earth is a flat island in the middle of an ocean chasm which keeps on backs of three whales. This island is the World Center round which, on heavenly spheres, different features rotate: the sun, the Moon, asterisks.
Those who thought differently, it was accepted to burn on fires. Now we became more civilised, on fires we burn nobody. But to put in you the two or fill up you at examination can very simply.
And the lesson of this history says: ALL can be mistaken. If ALL around will start to be hung up, I hope, you not begin to do the same? In other words, the opinion of one person or opinion of the majority of people CAN be ERRONEOUS. If we do not acquire this lesson of history, history to us it will give once again, and once again until we will not grow wiser. Apparently, the situation with division into a zero is a repetition of lesson already passed by us.
Now we will execute transformations and we will receive:
The first turned out line corresponds to a mathematical rule which says that if a zero to divide into any number, the zero as a result will turn out. Concerning the second line of mathematics speak, expression a zero to divide into a zero it is not meaningful, as cannot be defined. Hi-hi, and we have defined that the zero деленный on a zero equals to any number. To which number? And what number is necessary to you, such and write. By the way, one rich dad searched to itself in the firm of chief accountant. To all applicants, besides other, it asked a question: "How many will be twice two?". For work it has accepted the person who has answered this question with the question: "And how many it is necessary to you?".
And so, mathematicians want to see concrete number, instead of the general phrase as a result of division by zero. For this reason they consider division by zero impossible. Here it is a high time to remember the second lesson of history.
You about integrals heard? If is not present, it is not terrible. It looks so: the uncertain integral something equals to something plus a constant. What is "constant"? This any number which we do not know. Yes-yes, just the same unknown number, as well as result of division by zero. So, the integral is not meaningful? Has not only sense, but also it is often applied in engineering calculations. Focus consists that the uncertain integral is only the theory. In practical calculations certain integrals are applied. When business reaches the certain integrals, all problems with a constant, that is unknown number, disappear. As a result of integration quite concrete numbers turn out.
Why it is possible to find integral and to divide into a zero it is impossible? I think that in due time engineers have come to mathematicians on a throat and the decision of a concrete problem have demanded. Mathematicians have thought up integrals and ways of their finding. It has saved to mathematicians life.
Why engineers so will not make with division by zero? To the decision of practical problems with division by zero to our engineers still as to babies to pension. Engineers simply have not grown to this level of knowledge and technics. And to mathematicians division by zero and so will descend. What difference that you to learn? Nobel Prizes do not give to them so what for once again in vain to strain.
Considering the second lesson of history, it is possible to declare with all responsibility that arguments of mathematicians concerning impossibility of division by zero are not accepted, as in a similar case with uncertain integrals were them, mathematicians, are denied.
Division by zero is maybe. We are not able to divide into a zero yet. Anything shameful in it is not present. The third lesson of history. Once people in general were not able to divide. Even number on number. Anything, have learnt both to divide, and to integrate. We will learn and on a zero to divide. Certainly, if for it us will not burn on fires. Or to arrange round us wild dances of shamans under a tambourine, inspiring us the sacred spells "Division by zero it is impossible!", "Division by zero is not meaningful!".
We open a page of Wikipedia "Zero" (in Russian language) and attentively we read that to us offers collective reason. Mathematicians take number a and divide it into 0 (zero). Include the mathematical logic Further and begin reasonings. Let as a result of division the number c has turned out. In this case at number multiplication c by zero we should receive number a. But at multiplication to a zero of any number the zero as a result turns out. From this it follows that the number c cannot be result of division of number an by zero.
Personally I think hardly. We will try to write down all it easier:
a : 0 = c
c · 0 = a
Yes, really, not beautifully it turns out, especially wrong second equality. So in the mathematician does not happen. After all all know that any number increased by a zero, equals to zero.
Here it is a high time to remember a small lesson of history. Once, very long time ago, ALL considered that the Earth is a flat island in the middle of an ocean chasm which keeps on backs of three whales. This island is the World Center round which, on heavenly spheres, different features rotate: the sun, the Moon, asterisks.
 |
| Division by zero is maybe! |
And the lesson of this history says: ALL can be mistaken. If ALL around will start to be hung up, I hope, you not begin to do the same? In other words, the opinion of one person or opinion of the majority of people CAN be ERRONEOUS. If we do not acquire this lesson of history, history to us it will give once again, and once again until we will not grow wiser. Apparently, the situation with division into a zero is a repetition of lesson already passed by us.
a · 0 = 0
Now we will execute transformations and we will receive:
0 : a = 0
0 : 0 = a
The first turned out line corresponds to a mathematical rule which says that if a zero to divide into any number, the zero as a result will turn out. Concerning the second line of mathematics speak, expression a zero to divide into a zero it is not meaningful, as cannot be defined. Hi-hi, and we have defined that the zero деленный on a zero equals to any number. To which number? And what number is necessary to you, such and write. By the way, one rich dad searched to itself in the firm of chief accountant. To all applicants, besides other, it asked a question: "How many will be twice two?". For work it has accepted the person who has answered this question with the question: "And how many it is necessary to you?".
And so, mathematicians want to see concrete number, instead of the general phrase as a result of division by zero. For this reason they consider division by zero impossible. Here it is a high time to remember the second lesson of history.
You about integrals heard? If is not present, it is not terrible. It looks so: the uncertain integral something equals to something plus a constant. What is "constant"? This any number which we do not know. Yes-yes, just the same unknown number, as well as result of division by zero. So, the integral is not meaningful? Has not only sense, but also it is often applied in engineering calculations. Focus consists that the uncertain integral is only the theory. In practical calculations certain integrals are applied. When business reaches the certain integrals, all problems with a constant, that is unknown number, disappear. As a result of integration quite concrete numbers turn out.
Why it is possible to find integral and to divide into a zero it is impossible? I think that in due time engineers have come to mathematicians on a throat and the decision of a concrete problem have demanded. Mathematicians have thought up integrals and ways of their finding. It has saved to mathematicians life.
Why engineers so will not make with division by zero? To the decision of practical problems with division by zero to our engineers still as to babies to pension. Engineers simply have not grown to this level of knowledge and technics. And to mathematicians division by zero and so will descend. What difference that you to learn? Nobel Prizes do not give to them so what for once again in vain to strain.
Considering the second lesson of history, it is possible to declare with all responsibility that arguments of mathematicians concerning impossibility of division by zero are not accepted, as in a similar case with uncertain integrals were them, mathematicians, are denied.
Division by zero is maybe. We are not able to divide into a zero yet. Anything shameful in it is not present. The third lesson of history. Once people in general were not able to divide. Even number on number. Anything, have learnt both to divide, and to integrate. We will learn and on a zero to divide. Certainly, if for it us will not burn on fires. Or to arrange round us wild dances of shamans under a tambourine, inspiring us the sacred spells "Division by zero it is impossible!", "Division by zero is not meaningful!".
Enter number, how many there will be a factorial of three
"Enter number, how many there will be a factorial of three" Ogo! Here it is an ambush for blondes! Judging by that is written "enter number" is a site of any pervert from mathematics asks to enter into a window number. I would be frightened of such request! Same it is necessary to be such sadist that the visitors by means of a torture factorial to arrange! And it would be desirable to ask: "And you, the clever man, can count a factorial of four?! Or without the calculator poorly?!" Is not present, with this disgrace it is necessary to struggle. Anybody from Internet users is not obliged to know factorials - the Internet exists for all. It is obvious discrimination of blondes!
With a view of struggle against similar mathematical rudeness, we will create the small table of factorials for the aid to poor blondes and not only to it.
0! = 1
1! = 1
2! = 1 х 2 = 2
3! = 1 х 2 х 3 = 6
4! = 1 х 2 х 3 х 4 = 24
5! = 1 х 2 х 3 х 4 х 5 = 120
And so, the zero factorial is equal to unit, unit factorial is equal to unit, the factorial of two is equal to two, the factorial of three is equal six, the factorial of four is equal twenty four, the factorial of five is equal hundred twenty. I think, it will be quite enough for personal self-defence on the Internet.
By the way, as chance offers can ask those, who considers itself strongly literate, whether they know, how many figures at a factorial, well... For example, two hundred fifty five? In this number of five hundred five figures!!!
255! = 3350850684932979117652665123754814942022584063591740702576779884286208799035732771005626138126763314259280802118502282445926550135522251856727692533193070412811083330325659322041700029792166250734253390513754466045711240338462701034020262992581378423147276636643647155396305352541105541439434840109915068285430675068591638581980604162940383356586739198268782104924614076605793562865241982176207428620969776803149467431386807972438247689158656000000000000000000000000000000000000000000000000000000000000000
This number is five times longer, than the well-known number googol, in which only one unit and hundred zeroes. And at us five hundred five it is not simple zeroes, and different numbers)))
I hope, to anybody from you will not offer: "Enter number, how many there will be a factorial of two hundred fifty five")))
With a view of struggle against similar mathematical rudeness, we will create the small table of factorials for the aid to poor blondes and not only to it.
0! = 1
1! = 1
2! = 1 х 2 = 2
3! = 1 х 2 х 3 = 6
4! = 1 х 2 х 3 х 4 = 24
5! = 1 х 2 х 3 х 4 х 5 = 120
And so, the zero factorial is equal to unit, unit factorial is equal to unit, the factorial of two is equal to two, the factorial of three is equal six, the factorial of four is equal twenty four, the factorial of five is equal hundred twenty. I think, it will be quite enough for personal self-defence on the Internet.
By the way, as chance offers can ask those, who considers itself strongly literate, whether they know, how many figures at a factorial, well... For example, two hundred fifty five? In this number of five hundred five figures!!!
255! = 3350850684932979117652665123754814942022584063591740702576779884286208799035732771005626138126763314259280802118502282445926550135522251856727692533193070412811083330325659322041700029792166250734253390513754466045711240338462701034020262992581378423147276636643647155396305352541105541439434840109915068285430675068591638581980604162940383356586739198268782104924614076605793562865241982176207428620969776803149467431386807972438247689158656000000000000000000000000000000000000000000000000000000000000000
This number is five times longer, than the well-known number googol, in which only one unit and hundred zeroes. And at us five hundred five it is not simple zeroes, and different numbers)))
I hope, to anybody from you will not offer: "Enter number, how many there will be a factorial of two hundred fifty five")))
Thursday, February 03, 2011
Bermuda triangle and eternal youth
The Bermuda triangle is, we already spoke about it, when considered a triangle. With the Bermuda triangle it is connected a lot of mysterious and terrible stories. That in these stories truth, and that a usual advertising gimmick for advertising of favourite, - is difficult to understand. The Bermudas triangle on a card looks so:
We will not remember all stories connected with the Bermuda triangle, and to assort them on stones. On the Internet it is information full. We will consider only one, curious enough, a case connected with the Bermuda triangle.
The passenger plane "the Boeing 727" with passengers onboard from Atlantic ocean flies up to the airport of Miami. According to rules, the crew spends verification of hours with land services. In 20 minutes the plane disappears from screens of a radar. Radio contact to plane has interrupted. In 10 minutes after disappearance, the plane again appears on screens of a radar. The plane has safely landed. A whole hours passengers and the plane lagged behind for 10 minutes. Anybody from crew or passengers unusual has not noticed anything.
Truth it or fiction? Our habit always and all to say lies, and also the mania of government officials to code all, does not give us possibility precisely to answer this question. If it is fiction - it is a pity. If it is truth - before us interesting enough possibilities open.
Present that you have come to school. Today at you control on the mathematician. The lesson begins, the teacher gives out all the task. After that you imperceptibly get a small charm from the beautician, press a button - the teacher disappears. You easy solve all examples and problems. By the end of a lesson the teacher appears again. With astonishment looks at the watch in a class - shout, ор, but the lesson already comes to an end and it is necessary to collect examinations. Naturally, control all have written this perfectly well!
Whether it is possible to use such charm what to keep the youth? Yes. It is necessary simply most to disappear for some time. All around live, grow old - and you here are not present. It is possible to disappear for the period of vacation. And it is possible to disappear and for all academic year - how many the time you can save! Present, your girlfriends ugly old cows, and you - young and beautiful! Here the main thing - not to overdo. Passing employment, you risk to turn in обезьянку from a zoo. With you all will be photographed, feed you with bananas, and you nothing will not think from this that round you occurs.
And if it is serious, the similar charm will help to keep lives to people in extreme situations. For example, if urgent medical aid is necessary to the person, and this help it is necessary to wait. That the person has not died, you do so that it has disappeared and return it already after occurrence of doctors which can rescue this person.
Fantasy it or real possibility? From the point of view of mathematics here all speaks simply enough. If you have a desire in it to understand - write in comments. We can plunge into this mathematical jungle. But consider that mathematics specific enough science. Look how simply to become the millionaire from the point of view of mathematics: scrape out from a purse all money which at you are, and add to them one million dollars. All - you the proprietress of treasured one million. Where and as you this one million dollars take - mathematics at all does not excite. But the mathematics can prompt variants. It is possible to find one rich man which will give you one million. And it is possible to find one million not rich man which will give to you on one dollar, the same one million dollars as a result will turn out.
You ask, and how eternal youth? Elementary. Disappear from this world young and beautiful. Also do not come back any more never. Than this way differs from death? From our point of view - practically than. So for preservation of eternal youth it is necessary to look for other recipes.
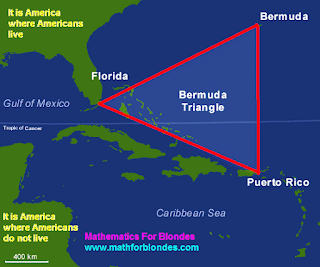 |
| Bermuda triangle |
We will not remember all stories connected with the Bermuda triangle, and to assort them on stones. On the Internet it is information full. We will consider only one, curious enough, a case connected with the Bermuda triangle.
The passenger plane "the Boeing 727" with passengers onboard from Atlantic ocean flies up to the airport of Miami. According to rules, the crew spends verification of hours with land services. In 20 minutes the plane disappears from screens of a radar. Radio contact to plane has interrupted. In 10 minutes after disappearance, the plane again appears on screens of a radar. The plane has safely landed. A whole hours passengers and the plane lagged behind for 10 minutes. Anybody from crew or passengers unusual has not noticed anything.
Truth it or fiction? Our habit always and all to say lies, and also the mania of government officials to code all, does not give us possibility precisely to answer this question. If it is fiction - it is a pity. If it is truth - before us interesting enough possibilities open.
Present that you have come to school. Today at you control on the mathematician. The lesson begins, the teacher gives out all the task. After that you imperceptibly get a small charm from the beautician, press a button - the teacher disappears. You easy solve all examples and problems. By the end of a lesson the teacher appears again. With astonishment looks at the watch in a class - shout, ор, but the lesson already comes to an end and it is necessary to collect examinations. Naturally, control all have written this perfectly well!
Whether it is possible to use such charm what to keep the youth? Yes. It is necessary simply most to disappear for some time. All around live, grow old - and you here are not present. It is possible to disappear for the period of vacation. And it is possible to disappear and for all academic year - how many the time you can save! Present, your girlfriends ugly old cows, and you - young and beautiful! Here the main thing - not to overdo. Passing employment, you risk to turn in обезьянку from a zoo. With you all will be photographed, feed you with bananas, and you nothing will not think from this that round you occurs.
And if it is serious, the similar charm will help to keep lives to people in extreme situations. For example, if urgent medical aid is necessary to the person, and this help it is necessary to wait. That the person has not died, you do so that it has disappeared and return it already after occurrence of doctors which can rescue this person.
Fantasy it or real possibility? From the point of view of mathematics here all speaks simply enough. If you have a desire in it to understand - write in comments. We can plunge into this mathematical jungle. But consider that mathematics specific enough science. Look how simply to become the millionaire from the point of view of mathematics: scrape out from a purse all money which at you are, and add to them one million dollars. All - you the proprietress of treasured one million. Where and as you this one million dollars take - mathematics at all does not excite. But the mathematics can prompt variants. It is possible to find one rich man which will give you one million. And it is possible to find one million not rich man which will give to you on one dollar, the same one million dollars as a result will turn out.
You ask, and how eternal youth? Elementary. Disappear from this world young and beautiful. Also do not come back any more never. Than this way differs from death? From our point of view - practically than. So for preservation of eternal youth it is necessary to look for other recipes.
Wednesday, February 02, 2011
Types of triangles
Types of triangles differ on clothes. Here when you look at the person, you, first of all, estimate it clothes and at once much becomes clear to you - what dirty trick from this person can be expected. Precisely as well at triangles. However, triangles have only two clothes which can be estimated simultaneously are corners and the parties. On a picture of a triangle it looks here so:
The very first triangle on a picture - a right triangle. It is called so because this triangle has one right angle. Two right angles at a triangle does not happen - remember the triangle theorem? Correctly, if two corners take away to themselves on 90 degrees, to the third corner nothing does not remain. And what can be a triangle with two corners? There are no two-coal triangles. Everything, the theorem of a right angle in a right triangle for blondes is proved!
It is possible to name a right triangle a triangle of Pythagor, on it Pythagor proved the well-known Pythagorean theorem. Let for Pythagor a right triangle also remains. Further on a picture at us the acute triangle is drawn. In it all three corners sharp, as female uvulas. Means, this triangle female. The top part of portrait gallery of triangles comes to an end with an obtuse triangle. This triangle has one big corner, and this corner stupid. It is a man's triangle. No, not because men stupid! No! Think. If there is a female triangle, means should be and man's. And all other triangles are already disassembled! There was only this... Here!
In the bottom part of a cloth of a brush of the unknown artist of the XXI-st century we see triangles which differ with lengths of the parties. To the first in the bottom number there is an equilateral triangle - a democracy symbol. Because all three parties at an equilateral triangle of equal length so - they are equal among themselves.
Further the isosceles triangle is drawn. A symbol of grace and beauty of women. At this triangle two parties have identical length. You imagine the woman with hips of different length? Here, and I do not represent. Why an isosceles triangle named so? In honour of blondes of whom mathematicians dreamt, drawing a pencil a triangle that under a hand has got. After all the majority of mathematicians there were no Leonardo's da Vinci's. Instead of fine Mona Liza's at them them isosceles triangles turned out.
The latest triangle - a scalene triangle - a symbol of geometrical tortures. And you thought, it is connected with erudition of this triangle? As though not so! At this triangle the teacher wants to know all three parties of different length and length of each of the parties of a triangle! After tortures by such triangle even Pythagor has not sustained and has told the theorem. In general, the scalene triangle is the most terrible nightmare of pupils on an extent already more than two thousand years.
Triangle names and pictures - it here. Types of triangles and their name.
 |
| Types of triangles |
The very first triangle on a picture - a right triangle. It is called so because this triangle has one right angle. Two right angles at a triangle does not happen - remember the triangle theorem? Correctly, if two corners take away to themselves on 90 degrees, to the third corner nothing does not remain. And what can be a triangle with two corners? There are no two-coal triangles. Everything, the theorem of a right angle in a right triangle for blondes is proved!
 |
| Types of triangles |
It is possible to name a right triangle a triangle of Pythagor, on it Pythagor proved the well-known Pythagorean theorem. Let for Pythagor a right triangle also remains. Further on a picture at us the acute triangle is drawn. In it all three corners sharp, as female uvulas. Means, this triangle female. The top part of portrait gallery of triangles comes to an end with an obtuse triangle. This triangle has one big corner, and this corner stupid. It is a man's triangle. No, not because men stupid! No! Think. If there is a female triangle, means should be and man's. And all other triangles are already disassembled! There was only this... Here!
In the bottom part of a cloth of a brush of the unknown artist of the XXI-st century we see triangles which differ with lengths of the parties. To the first in the bottom number there is an equilateral triangle - a democracy symbol. Because all three parties at an equilateral triangle of equal length so - they are equal among themselves.
Further the isosceles triangle is drawn. A symbol of grace and beauty of women. At this triangle two parties have identical length. You imagine the woman with hips of different length? Here, and I do not represent. Why an isosceles triangle named so? In honour of blondes of whom mathematicians dreamt, drawing a pencil a triangle that under a hand has got. After all the majority of mathematicians there were no Leonardo's da Vinci's. Instead of fine Mona Liza's at them them isosceles triangles turned out.
The latest triangle - a scalene triangle - a symbol of geometrical tortures. And you thought, it is connected with erudition of this triangle? As though not so! At this triangle the teacher wants to know all three parties of different length and length of each of the parties of a triangle! After tortures by such triangle even Pythagor has not sustained and has told the theorem. In general, the scalene triangle is the most terrible nightmare of pupils on an extent already more than two thousand years.
Triangle names and pictures - it here. Types of triangles and their name.
Mathematics of an inequality
In the mathematician equalities and inequalities are very extended. Whether the inequality can be useful practically to us in an everyday life? Perhaps if you learn to make inequalities of the most simple situations and to analyze them.
Here the most usual situation. You have got acquainted with the guy who was presented to Vasej. Вася has told that it the friend Bill Gates. Here we also will use mathematical principles of construction and the inequality analysis.
First of all, we will remember one mathematical rule - an addition rule. This rule says that from shift composed the sum does not change. Other mathematical rule asserts that at shift of factors product does not change. Here we apply this principle of shift to words of Vasi and we look that at us it has turned out:
(Vasja has told that it the friend Bill Gates) is equal (Bill Gates has told that Vasja its friend)
Now we will analyse both received phrases. You personally are not familiar neither with Vasej, nor with Bill Gates. But Bill Gates - the celebrated personality, therefore you will trust its words much more, than to words of known Vasi any to nobody. The probability of that Vasja REALLY is the friend Bill Gates, is smallest. Hence, we have received an inequality which looks so:
(Vasja has told that it the friend Bill Gates) is not equal (Bill Gates has told that Vasja its friend)
From the phrase analysis it is possible to draw a conclusion that from you something is necessary for this Vasja. If simply to make upon you impression is one. If speech comes about money is another.
Similar reception - to be called as someone concerning the celebrated personality - any swindlers very often use. Especially, when speech comes about money: "the pupil such", "the right hand of that" and so on, and so forth.
If you learn easily and quickly to define situation high lights, mentally to change a situation on opposite and to analyze the received results, it will be much easier to you to make correct decisions.
Here the most usual situation. You have got acquainted with the guy who was presented to Vasej. Вася has told that it the friend Bill Gates. Here we also will use mathematical principles of construction and the inequality analysis.
First of all, we will remember one mathematical rule - an addition rule. This rule says that from shift composed the sum does not change. Other mathematical rule asserts that at shift of factors product does not change. Here we apply this principle of shift to words of Vasi and we look that at us it has turned out:
(Vasja has told that it the friend Bill Gates) is equal (Bill Gates has told that Vasja its friend)
Now we will analyse both received phrases. You personally are not familiar neither with Vasej, nor with Bill Gates. But Bill Gates - the celebrated personality, therefore you will trust its words much more, than to words of known Vasi any to nobody. The probability of that Vasja REALLY is the friend Bill Gates, is smallest. Hence, we have received an inequality which looks so:
(Vasja has told that it the friend Bill Gates) is not equal (Bill Gates has told that Vasja its friend)
From the phrase analysis it is possible to draw a conclusion that from you something is necessary for this Vasja. If simply to make upon you impression is one. If speech comes about money is another.
Similar reception - to be called as someone concerning the celebrated personality - any swindlers very often use. Especially, when speech comes about money: "the pupil such", "the right hand of that" and so on, and so forth.
If you learn easily and quickly to define situation high lights, mentally to change a situation on opposite and to analyze the received results, it will be much easier to you to make correct decisions.
Subscribe to:
Posts (Atom)
















